题目内容
问题:如图1,在正方形ABCD内有一点P,PA=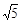 ,PB=
,PB=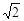 ,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
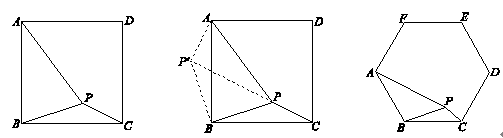
请你参考小明同学的思路,解决下列问题:
(1) 图2中∠BPC的度数为 ;
(2) 如图3,若在正六边形ABCDEF内有一点P,且PA=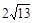 ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
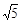 ,PB=
,PB=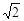 ,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
请你参考小明同学的思路,解决下列问题:
(1) 图2中∠BPC的度数为 ;
(2) 如图3,若在正六边形ABCDEF内有一点P,且PA=
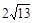 ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .(1)135° (2) 120° 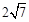
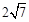
试题分析:解:(1)135°;………………………………………………………………………… 2分
(2)120°;………………………………………………………………………… 3分
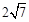 . ……………………………………………………………………… 5分
. ……………………………………………………………………… 5分点评:解答此题的关键,是进行巧妙地旋转变换。让每一点P绕一固定点(固定轴线)旋转一个定角,变成另一点P′,如此产生的变换称为平面上(空间中)的旋转变换,它是欧氏几何中的一种重要变换,是解答解析几何数学题的一种重要思想。

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目


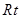 △
△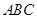 中,∠
中,∠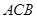 =90o,
=90o,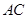 =
=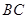 =1,将
=1,将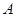 点逆时针旋转30o后得到
点逆时针旋转30o后得到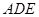 ,点
,点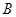 经过的路径为弧
经过的路径为弧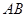 ,则图中阴影部分的面积是 。(结果用
,则图中阴影部分的面积是 。(结果用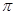 表示)
表示)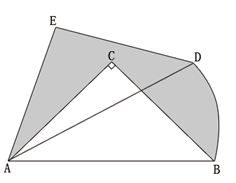
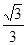 a
a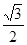 a
a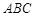 内接于圆
内接于圆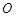 ,动点
,动点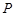 在圆上,且不与B、C重合,则
在圆上,且不与B、C重合,则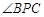 等于( )
等于( )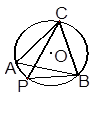
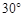 B.
B.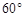 C.60°或120° D. 120°
C.60°或120° D. 120°
 中,∠C=90°.
中,∠C=90°.