题目内容
如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.

(1)DE=BD;(2)4.8
试题分析:(1)连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.
(2)由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC•BE=CB•AD.进而求出BE的长.
(1)如图,连接AD,则AD⊥BC,

在等腰三角形ABC中,AD⊥BC,
∴∠CAD=∠BAD(等腰三角形三线合一),
∴弧ED=弧BD,
∴DE=BD;
(2)∵AB=5,BD=
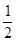 BC=3,
BC=3,∴AD=4,
∵AB=AC=5,
∴AC•BE=CB•AD,
∴BE=4.8.
点评:用等腰三角形三线合一的特点得出圆周角相等是解答本题的关键.

练习册系列答案
相关题目

 ∠BAC
∠BAC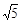 ,PB=
,PB=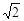 ,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.
,PC=1,求∠BPC的度数.小明同学的想法是:已知条件比较分散,可以通过旋转变换将分散的已知条件集中在一起,于是他将△BPC绕点B逆时针旋转90°,得到了△BP′A(如图2),然后连结PP′.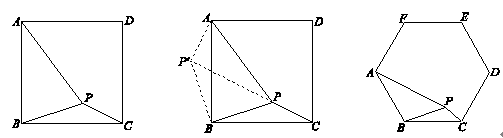
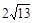 ,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
,PB=4,PC=2,则∠BPC的度数为 ,正六边形ABCDEF的边长为 .
 ,
, ,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.
,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.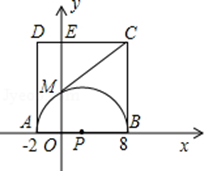
 周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.
周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.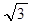 =1.732,
=1.732,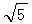 =2.236,结果精确到0.01km.)
=2.236,结果精确到0.01km.)