题目内容
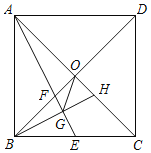
【题目】如图,正方形ABCD中,对角线AC、BD相交于点O,点E是BC的中点,AE交BD于点F,BH⊥AE于点G,连接OG,则下列结论中①OF=OH,②△AOF∽△BGF,③tan∠GOH=2,④FG+CH=![]() GO,正确的个数是( )
GO,正确的个数是( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
①根据正方形ABCD的性质,可得AC⊥BD,∠AOF=∠BOH=90°,又BH⊥AE,∠AFO=∠BFG,即∠OAF=∠OBH,进而可证△AOF≌△BOH(ASA),即OF=OH.
②根据∠AOF=∠BGF=90°,∠OAF=∠OBH,可得△AOF∽△BGF
③根据点E是BC的中点,可得AB=BC=2BE,又因为∠AOB=∠AGB=90°,故A、B、G、O四点共圆,由圆周角定理推论可知∠BOG=∠BAE,∠AGO=∠ABO=45°,由∠BOG+∠GOH=90°,∠BAE+∠AEB=90°,可得∠GOH=∠AEB,求得tan∠GOH=tan∠AEB=![]() =2
=2
④根据正方形的性质可得到△ADF∽△EBF,即![]() =
=![]() =2,即DF=2BF,可求得OF+OD=2(OD﹣OF),即OF=
=2,即DF=2BF,可求得OF+OD=2(OD﹣OF),即OF=![]() OD=
OD=![]() OB,OH=
OB,OH=![]() OB=
OB=![]() OC,CH=
OC,CH=![]() OC=
OC=![]() AB,由∠AGO=∠ACE=45°,∠OAG=∠EAC,得到△AOG∽△AEC,即
AB,由∠AGO=∠ACE=45°,∠OAG=∠EAC,得到△AOG∽△AEC,即![]() =
=![]()
根据勾股定理AE=![]() =
=![]() AB,可求得OG=
AB,可求得OG=![]() =
=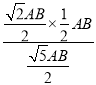 =
=![]() AB,
AB,![]() GO=
GO=![]() AB.根据△AOF∽△BGF,△AOF≌△BOH得△BGF∽△BOH,即
AB.根据△AOF∽△BGF,△AOF≌△BOH得△BGF∽△BOH,即![]() =
=![]() ,由BG=
,由BG=![]() =
=![]() AB,得
AB,得![]() =
=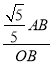 ,解得:FG=
,解得:FG=![]() AB,故FG+CH=
AB,故FG+CH=![]() AB+
AB+![]() AB≠
AB≠![]() GO=
GO=![]() AB.
AB.
解:∵四边形ABCD是正方形,
∴AC⊥BD,AB=BC=AD,OA=OB=OC=OD,AD∥BC,∠ABO=∠ACB=45°,
∴∠AOF=∠BOH=90°,
∵BH⊥AE,∠AFO=∠BFG,
∴∠OAF=∠OBH,
在△AOF和△BOH中,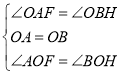 ,
,
∴△AOF≌△BOH(ASA),
∴OF=OH,①正确;
∵∠AOF=∠BGF=90°,∠OAF=∠OBH,
∴△AOF∽△BGF,②正确;
∵点E是BC的中点,
∴AB=BC=2BE,
∵∠AOB=∠AGB=90°,
∴A、B、G、O四点共圆,
∴∠BOG=∠BAE,∠AGO=∠ABO=45°,
∵∠BOG+∠GOH=90°,∠BAE+∠AEB=90°,
∴∠GOH=∠AEB,
∴tan∠GOH=tan∠AEB=![]() =2,③正确;
=2,③正确;
∵AD∥BC,
∴△ADF∽△EBF,
∴![]() =
=![]() =2,
=2,
∴DF=2BF,
∴OF+OD=2(OD﹣OF),
解得:OF=![]() OD=
OD=![]() OB,
OB,
∴OH=![]() OB=
OB=![]() OC,
OC,
∴CH=![]() OC=
OC=![]() AB,
AB,
∵∠AGO=∠ACE=45°,∠OAG=∠EAC,
∴△AOG∽△AEC,
∴![]() =
=![]()
∵AE=![]() =
=![]() AB,
AB,
∴OG=![]() =
=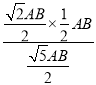 =
=![]() AB,
AB,
∴![]() GO=
GO=![]() AB,
AB,
∵△AOF∽△BGF,△AOF≌△BOH,
∴△BGF∽△BOH,
∴![]() =
=![]() ,
,
∵BG=![]() =
=![]() AB,
AB,
∴![]() =
=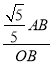
解得:FG=![]() AB,
AB,
∴FG+CH=![]() AB+
AB+![]() AB≠
AB≠![]() GO=
GO=![]() AB,④错误;
AB,④错误;
正确的个数有3个,
故选:C.