ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΙϊΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χax2+bx+cΘΫ0”–2Ηω Β ΐΗυΘ§«“Τδ÷–“ΜΗω Β ΐΗυ «Νμ“ΜΗω Β ΐΗυΒΡ3±ΕΘ§‘ρ≥ΤΗΟΖΫ≥ΧΈΣΓΑΝΔΗυΖΫ≥ΧΓ±Θ°
Θ®1Θ©ΖΫ≥Χx2©¹4x+3ΘΫ0ΓΓ ΝΔΗυΖΫ≥ΧΘ§ΖΫ≥Χx2©¹2x©¹3ΘΫ0ΓΓ ΝΔΗυΖΫ≥ΧΘΜΘ®«κΧνΓΑ «Γ±ΜρΓΑ≤Μ «Γ±Θ©
Θ®2Θ©«κ÷ΛΟςΘΚΒ±ΒψΘ®mΘ§nΘ©‘ΎΖ¥±»άΐΚ· ΐy![]() …œ ±Θ§ΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2+4x+nΘΫ0 «ΝΔΗυΖΫ≥ΧΘΜ
…œ ±Θ§ΙΊ”ΎxΒΡ“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2+4x+nΘΫ0 «ΝΔΗυΖΫ≥ΧΘΜ
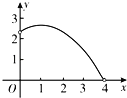
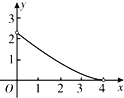
Θ®3Θ©»τΖΫ≥Χax2+bx+cΘΫ0 «ΝΔΗυΖΫ≥ΧΘ§«“ΝΫΒψPΘ®3Θ§2Θ©ΓΔQΘ®6Θ§2Θ©Ψυ‘ΎΕΰ¥ΈΚ· ΐyΘΫax2+bx+c…œΘ§«σΖΫ≥Χax2+bx+cΘΫ0ΒΡΝΫΗωΗυΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ© «Θ§≤Μ «ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©x1ΘΫ![]() , x2=
, x2=![]()
ΓΨΫβΈωΓΩ
Θ®1Θ©Ζ÷±πΫβΖΫ≥Χx2-4x+3=0”κx2-2x-3=0Θ§«σ≥ωΥϋΟ«ΒΡΗυΘ§ΗυΨίΓΑΝΔΗυΖΫ≥ΧΓ±ΒΡΕ®“εΘ§≈–ΕœΥϋΟ« «≤Μ «ΝΔΗυΖΫ≥ΧΘ°
Θ®2Θ©”…ΒψΘ®mΘ§nΘ©‘ΎΖ¥±»άΐΚ· ΐy=![]() ΒΡΆΦœσ…œΘ§ΒΟΒΫmn=3Θ§ΫβΖΫ≥Χmx2+4x+n=0«σΒΟx1”κx2ΒΡ÷ΒΘ§≈–Εœ «≤Μ «ΝΔΗυΖΫ≥ΧΘ°
ΒΡΆΦœσ…œΘ§ΒΟΒΫmn=3Θ§ΫβΖΫ≥Χmx2+4x+n=0«σΒΟx1”κx2ΒΡ÷ΒΘ§≈–Εœ «≤Μ «ΝΔΗυΖΫ≥ΧΘ°
Θ®3Θ©”…ΖΫ≥Χax2+bx+c=0 «ΝΔΗυΖΫ≥ΧΘ§ΒΟΒΫx1=3x2Θ§”…ΉίΉχ±ξœύΆ§ΒΡΝΫΒψPΘ®3Θ§2Θ©ΓΔQΘ®6Θ§2Θ©ΕΦ‘Ύ≈ΉΈοœΏy=ax2+bx+c…œΘ§ΗυΨί≈ΉΈοœΏΒΡΕ‘≥Τ÷αΒΟΒΫx1+x2ΘΫ9Θ§¥”Εχ«σ≥ωΖΫ≥ΧΒΡΝΫΗωΗυΘ°
ΫβΘΚΘ®1Θ©ΫβΖΫ≥Χx2-4x+3=0Θ§ΒΟΘΚx1=3Θ§x2=1Θ§
ΓΏx1=3x2Θ§
ΓύΖΫ≥Χx2-4x+3=0 «ΝΔΗυΖΫ≥ΧΘΜ
ΫβΖΫ≥Χx2-2x-3=0Θ§ΒΟΘΚx1=3Θ§x2=-1Θ§
ΓΏx1=-3x2Θ§
ΓύΖΫ≥Χx2-2x-3=0≤Μ «ΝΔΗυΖΫ≥ΧΘ°
Ι ¥πΑΗΈΣΘΚ «Θ§≤Μ «Θ°
Θ®2Θ©ΓΏΒψΘ®m,nΘ©‘ΎΖ¥±»άΐΚ· ΐ![]() …œΘ§Υυ“‘
…œΘ§Υυ“‘![]()
”Ο«σΗυΙΪ ΫΫβΖΫ≥ΧΒΟΘΚ![]()
x1ΘΫ©¹![]() Θ§x2ΘΫ©¹
Θ§x2ΘΫ©¹![]() Θ§
Θ§
Γύx1ΘΫ3x2Θ§
Β±ΒψΘ®mΘ§nΘ©‘ΎΖ¥±»άΐΚ· ΐyΘΫ![]() …œ ±Θ§“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2+4x+nΘΫ0 «ΝΔΗυΖΫ≥ΧΘΜ
…œ ±Θ§“Μ‘ΣΕΰ¥ΈΖΫ≥Χmx2+4x+nΘΫ0 «ΝΔΗυΖΫ≥ΧΘΜ
Θ®3Θ©ΓΏΖΫ≥Χax2+bx+cΘΫ0 «ΝΔΗυΖΫ≥ΧΘ§Γύ…ηx1ΘΫ3x2Θ§
ΓΏPΘ®3Θ§2Θ©Θ§QΘ®6Θ§2Θ©‘Ύ≈ΉΈοœΏyΘΫax2+bx+c…œΘ§
Γύ≈ΉΈοœΏΒΡΕ‘≥Τ÷α![]() Θ§
Θ§
Γύx1+x2ΘΫ9Θ§Γύ3x2+x2ΘΫ9Θ§Γύx2=![]() Θ§Γύx1ΘΫ3x2ΘΫ
Θ§Γύx1ΘΫ3x2ΘΫ![]() Θ°
Θ°
Υυ“‘ΖΫ≥Χax2+bx+cΘΫ0ΒΡΝΫΗωΗυΈΣΘΚx1ΘΫ![]() , x2=
, x2=![]()

 Ή÷¥ ΨδΤΣ”κΆ§≤ΫΉςΈΡ¥ο±ξœΒΝ–¥πΑΗ
Ή÷¥ ΨδΤΣ”κΆ§≤ΫΉςΈΡ¥ο±ξœΒΝ–¥πΑΗ