题目内容
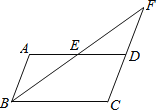
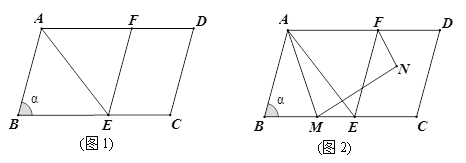
【题目】如图1,在□ABCD中,AB=6,∠B= ![]() (60°<
(60°<![]() ≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
≤90°). 点E在BC上,连接AE,把△ABE沿AE折叠,使点B与AD上的点F重合,连接EF.
(1)求证:四边形ABEF是菱形;
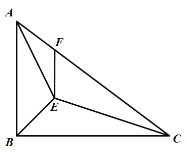
(2)如图2,点M是BC上的动点,连接AM,把线段AM绕点M顺时针旋转![]() 得到线段MN,连接FN,求FN的最小值(用含
得到线段MN,连接FN,求FN的最小值(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)详见解析;(2)FE·sin(![]()
![]() -90°)
-90°)
【解析】
(1)由四边形ABCD是平行四边形得AF∥BE,所以∠FAE=∠BEA,由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA,所以∠BAE=∠FEA,故有AB∥FE,因此四边形ABEF是平行四边形,又BE=EF,因此可得结论;
(2)根据点M在线段BE上和EC上两种情况证明∠ENG=90°-![]()
![]() ,利用菱形的性质得到∠FEN=
,利用菱形的性质得到∠FEN=![]()
![]() -90°,再根据垂线段最短,求出FN的最小值即可.
-90°,再根据垂线段最短,求出FN的最小值即可.
(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠BEA,
由折叠的性质得∠BAE=∠FAE,∠BEA=∠FEA, BE=EF,
∴∠BAE=∠FEA,
∴AB∥FE,
∴四边形ABEF是平行四边形,
又BE=EF,
∴四边形ABEF是菱形;
(2)①如图1,当点M在线段BE上时,在射线MC上取点G,使MG=AB,连接GN、EN.
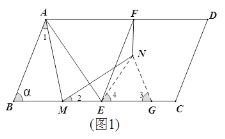
∵∠AMN=∠B=![]() ,∠AMN+∠2=∠1+∠B
,∠AMN+∠2=∠1+∠B
∴∠1=∠2
又AM=NM,AB=MG
∴△ABM≌△MGN
∴∠B=∠3,NG=BM
∵MG=AB=BE
∴EG=AB=NG
∴∠4=∠ENG=![]() (180°-
(180°-![]() )=90°-
)=90°-![]()
![]()
又在菱形ABEF中,AB∥EF
∴∠FEC=∠B=![]()
∴∠FEN=∠FEC-∠4=![]() - (90°-
- (90°-![]()
![]() )=
)=![]()
![]() -90°
-90°
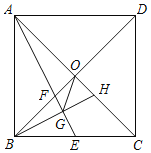
②如图2,当点M在线段EC上时,在BC延长线上截取MG=AB,连接GN、EN.
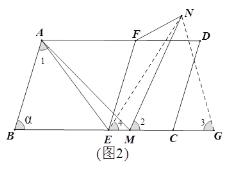
同理可得:∠FEN=∠FEC-∠4=![]() - (90°-
- (90°-![]()
![]() )=
)=![]()
![]() -90°
-90°
综上所述,∠FEN=![]()
![]() -90°
-90°
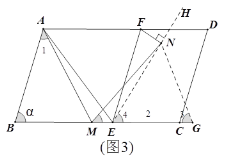
∴当点M在BC上运动时,点N在射线EH上运动(如图3)
当FN⊥EH时,FN最小,其最小值为FE·sin(![]()
![]() -90°)
-90°)

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案