题目内容
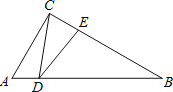
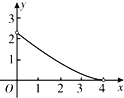
【题目】如图,抛物线![]() 与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
与x轴交于点A,B两点(点A在点B左边),与y轴交于点C.
(1)求A,B两点的坐标.
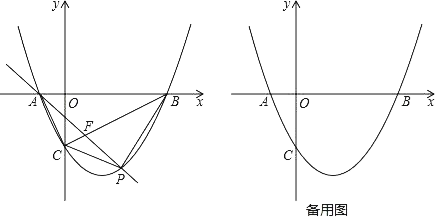
(2)点P是线段BC下方的抛物线上的动点,连结PC,PB.
①是否存在一点P,使△PBC的面积最大,若存在,请求出△PBC的最大面积;若不存在,试说明理由.
②连结AC,AP,AP交BC于点F,当∠CAP=∠ABC时,求直线AP的函数表达式.
【答案】(1)A、B的坐标分别为(﹣1,0)、(4,0);(2)①存在,见解析,面积的最大值为4,②![]() .
.
【解析】
(1)令y=0,则x=1或-4,令x=0,则y=2,即可求解;
(2)①S△PBC=![]() ×PH×OB,即可求解;
×PH×OB,即可求解;
②证明△ACF∽△BCA,求得:CF=![]() ,BF=BC-CF=
,BF=BC-CF=![]() ,由BF2=(m-4)2+(
,由BF2=(m-4)2+(![]() m-2)2=(
m-2)2=(![]() )2,即可求解.
)2,即可求解.
(1)令y=0,则x=1或﹣4,令x=0,则y=2,
即点A、B、C的坐标分别为(﹣1,0)、(4,0)、(0,﹣2);
(2)①存在,理由:过点P作HP∥y轴交BC于点H,
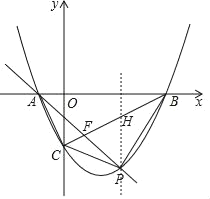
将点B、C的坐标代入一次函数表达式y=kx+b得:![]() ,解得:
,解得: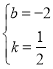 ,
,
故直线BC的表达式为:y=![]() x﹣2,
x﹣2,
设点P坐标为(x,![]() )、H(x,
)、H(x,![]() x﹣2),
x﹣2),
S△PBC=![]() ×PH×OB=
×PH×OB=![]() ×(
×(![]() x﹣2
x﹣2![]() )×4=﹣x2+4x,
)×4=﹣x2+4x,
∵﹣1<0,故S△PBC有最大值,
当x=2时,面积的最大值为4,此时点P(2,﹣3);
②∠CAP=∠ABC,∠ACF=∠ACF,∴△ACF∽△BCA,
∴AC2=BCCF,其中AC=![]() ,BC=2
,BC=2![]() ,
,
故:CF=![]() ,BF=BC﹣CF=
,BF=BC﹣CF=![]() ,
,
设点F的坐标为(m,![]() m﹣2),
m﹣2),
则:BF2=(m﹣4)2+(![]() m﹣2)2=(
m﹣2)2=(![]() )2,
)2,
解得:m=1或7(舍去m=7),
故点F坐标(1,﹣![]() ),
),
将点A、F坐标代入一次函数表达式y=kx+b,
同理可得:直线AF(或直线AP)的表达式为:y=﹣![]() x﹣
x﹣![]() .
.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案