题目内容
【题目】如图，已知抛物线y=ax2+
x+c与x轴交于A，B两点，与y轴交于C点，且A(2，0)，C(0，-4)，直线l：y=-
x-4与x轴交于点D，点P是抛物线y=ax2+x+c上的一动点，过点P作PE⊥x轴，垂足为E，交直线l于F．
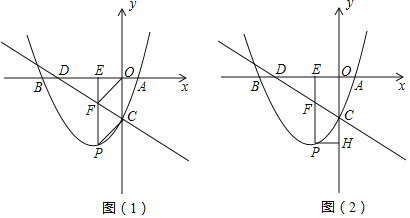
(1)试求该抛物线表达式；
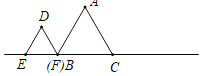
(2)如图(1)，若点P在第三象限，四边形PCOF是平行四边形，求P点的坐标；
(3)如图(2)，连接AC．求证：△ACD是直角三角形．
【答案】(1)y=
x2+
x-4；(2)P点的坐标为(-8，-4)，(-2.5，-
)；(3)证明见解析.
【解析】
（1）利用待定系数法即可求a、c的值，从而求得抛物线的表达式;
（2）设P点的坐标是（x，
x2+
x-4），则F（x，-
x-4），由OCPF是平行四边形得OC=FP,OC∥PF，从而-x2-
x=4，求解即可得P的横坐标，代入解析式即可得P的坐标．
（3）分别求出点A、C、D的坐标，可以根据勾股定理的逆定理即可判断
(1)依题意，抛物线经过A(2，0)，C(0，-4)，则c=-4
将点A代入得0=4a+×2-4，解得a=
抛物线的解析式是y=x2+x-4
(2)设P点的坐标是(x，x2+x-4)，则F(x，-x-4)
∴PF=(-x-4)-(x2+x-4)=-x2-x
∵四边形OCPF是平行四边形
∴OC=FP，OC∥PF
∴-x2-x=4
即2x2+21x+40=0
解得x1=-8x2=-2.5
∴P点的坐标为(-8，-4)，(-2.5，-
)
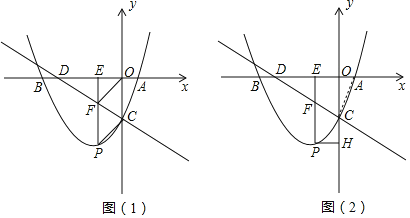
(3)当y=0时，-x-4=0，得x=-8，即D(-8，0)
当x=0时，0-4=y，即C(0，-4)
当y=0时，x2+x-4=0
解得x1=-10x2=2，即B(-10，0)，A(2，0)
∴AD=10
∵AC2=22+42=20
CD2=82+42=80
∴AD2=AC2+CD2
∴∠ACD=90°△ACD是直角三角形
