题目内容
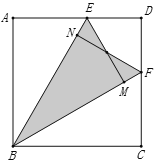
【题目】如图，在
中，
，
，
，点D、E分别是BC、AD的中点，
交CE的延长线于点F，则四边形AFBD的面积为______．
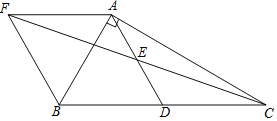
【答案】12
【解析】分析：根据三角函数得出AC的长度，然后根据中点的性质得出△AEF和△DEC全等，从而得出AF=DC，根据平行线间的距离相等得出△ABF的面积和△ADC的面积相等，从而得出答案．
详解：∵AB=4，
， ∴AC=6，∵E为FC的中点， ∴EF=CE，∵AF∥BC，
∴∠AFE=∠DCE， 又∵∠AEF=∠DEC， ∴△AEF≌△DEC， ∴AF=DC，
∴△ABF的面积和△ADC的面积相等， ∴四边形AFBD的面积等于△ABC的面积，
∴S=4×6÷2=12， 即四边形AFBD的面积为12．
练习册系列答案
相关题目
