题目内容
如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA。
(1)试求∠DAE的度数。
(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?试说明理由。
(1)试求∠DAE的度数。
(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?试说明理由。

(1)∠DAE=45°;(2)∠DAE的度数不变
试题分析:(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,根据等边对等角的性质求出∠BAD=∠BDA,∠E=∠CAE,再根据三角形的一个外角等于和它不相邻的两个内角的和即可求出∠DAE的度数;
(2)由BD=BA可得∠BAD=∠BDA=
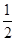 (180°-∠B),由CE=CA可得∠E=∠CAE=
(180°-∠B),由CE=CA可得∠E=∠CAE=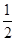 ∠ACB=
∠ACB=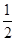 (90°-∠B),再根据三角形外角的性质即可得到结论。
(90°-∠B),再根据三角形外角的性质即可得到结论。(1)∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵BD=BA,
∴∠BAD=∠BDA=
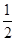 (180°-45°)=67.5°,
(180°-45°)=67.5°,∵CE=CA,
∴∠E=∠CAE=
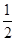 ×45°=22.5°,
×45°=22.5°,∴∠DAE=∠BDA-∠E=67.5°-22.5°=45°;
(2)∵BD=BA,
∴∠BAD=∠BDA=
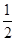 (180°-∠B),
(180°-∠B),∵CE=CA,
∴∠E=∠CAE=
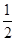 ∠ACB=
∠ACB=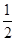 (90°-∠B),
(90°-∠B),∴∠DAE=∠BDA-∠E=
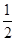 (180°-∠B)-
(180°-∠B)-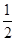 (90°-∠B)=90°-
(90°-∠B)=90°-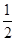 ∠B-45°+
∠B-45°+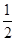 ∠B=45°,
∠B=45°,即∠DAE的度数不变.
点评:解答本题的关键是熟练掌握三角形外角的性质:三角形的一个外角等于与它不相邻的两个内角的和。

练习册系列答案
相关题目
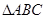 中,点
中,点 为
为 边上的一点,
边上的一点,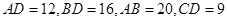 .
.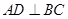 .
.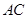 的长及
的长及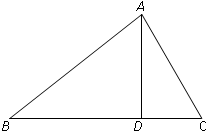
 的距离是()
的距离是()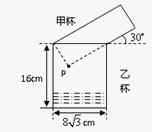
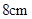

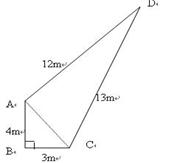
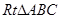 两边为3,4,则第三边长________。
两边为3,4,则第三边长________。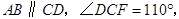 且
且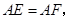 求
求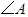 的度数.
的度数.