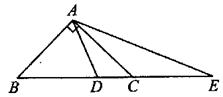
题目内容
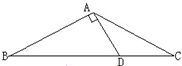
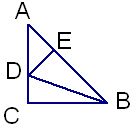
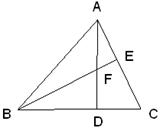
如图所示,在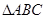 中,点
中,点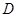 为
为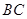 边上的一点,
边上的一点,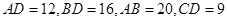 .
.
(1)试说明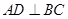 .
.
(2)求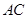 的长及
的长及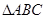 的面积.
的面积.
(2)判断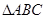 是否是直角三角形,并说明理由.
是否是直角三角形,并说明理由.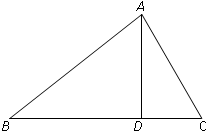
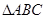 中,点
中,点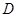 为
为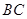 边上的一点,
边上的一点,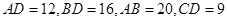 .
.(1)试说明
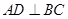 .
.(2)求
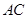 的长及
的长及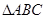 的面积.
的面积.(2)判断
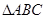 是否是直角三角形,并说明理由.
是否是直角三角形,并说明理由.
(1)见解析;(2)15,150;(3)是
试题分析:(1)根据勾股定理的逆定理即可判断;
(2)先根据勾股定理求得斜边的长,再根据直角三角形的面积公式即可求得结果;
(3)根据勾股定理的逆定理即可判断.
(1)
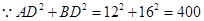
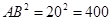
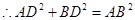
∴
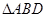 是直角三角形
是直角三角形∴
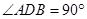 即
即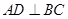 ;
; (2)∵
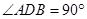 ,且点
,且点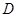 为
为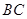 边上的一点
边上的一点∴
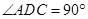
∴由勾股定理得:
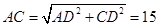
∴
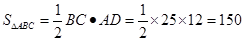 ;
; (3)
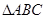 是直角三角形
是直角三角形 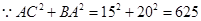 ,
, 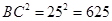
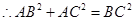
∴
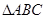 是直角三角形.
是直角三角形.点评:解答本题的根据是熟练掌握勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形.

练习册系列答案
相关题目
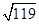 .
.