Question

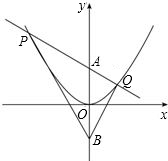
如图①，在平面直角坐标系中，AB、CD都垂直于x轴，垂足为B、D，且AD与BC相交于E点．已知：A（-2，-6），C（1，-3）
（1）求证：E点在y轴上；
（2）如果AB的位置不变，而DC水平向右移动K（K＞0）个单位，此时AD与BC相交于E′点，如图②，求△AE′C的面积S关于K的函数解析式；
（3）过A、E、E′三点的抛物线中，是否存在一条抛物线，它的顶点在x轴上？若存在，请求出k的值；若不存在，说明理由．

Answer 1

（1）证明：根据题意得：B（-2，0），点D（1，0），
设直线AD的解析式为：y=kx+b，
∴

-2k+b=-6 k+b=0

，
解得：

k=2 b=-2

，
∴直线AD的解析式为：y=2x-2，
同理可得：直线BC的解析式为：y=-x-2，
∵2x-2=-x-2，
解得：x=0，y=-2，
∴AD与BC的交点E的坐标为（0，-2）；
∴E点在y轴上；

（2）由（1）当DC水平向右平移k后，过AD与BC的交点E′作E′F⊥x轴垂足为F．
同（1）可得：

E′F

AB

+

E′F

DC

=1，得：E′F=2，
∵BA∥DC，
∴S_△BCA=S_△BDA，
∴S_△AE′C=S_△BDE′=

1

2

BD•E′F=

1

2

（3+k）×2=3+k，
∴S=3+k为所求函数解析式．

（3）存在．
设抛物线的方程y=ax²+bx+c（a≠0）过A（-2，-6），C（1，-3），E（0，-2）三点，
得方程组

4a-2b+c=-6 a+b+c=-3 c=-2

，
解得a=-1，b=0，c=-2，
∴抛物线方程y=-x²-2
（注：题目未告之E（0，-2）是抛物线的顶点）