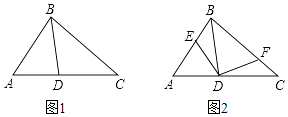Question

【题目】综合与实践：折纸中的数学
动手操作：
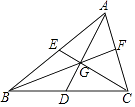
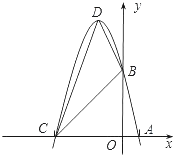
如图，将矩形ABCD折叠，点B落在AD边上的点B′处，折痕为GH，再将矩形ABCD折叠，点D落在B′H的延长线上，对应点为D′，折痕为B′E，延长GH于点F，O为GE的中点．
数学思考：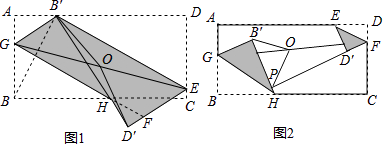

（1）猜想：线段OB′与OD′的数量关系是（不要求说理或证明）．
（2）求证：四边形GFEB′为平行四边形；
（3）拓展探究：
如图2，将矩形ABCD折叠，点B对应点B′，点D对应点为D′，折痕分别为GH、EF，∠BHG=∠DEF，延长FD′交B′H于点P，O为GF的中点，试猜想B′O与OP的数量关系，并说明理由．

Answer 1

【答案】
（1）OB′=OD′
（2）

解：如图1，

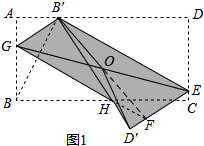
由折叠得：∠GHB=∠GHB′= ∠B′HB，

∠DB′E=∠D′B′E= ∠D′B′D，

∵四边形ABCD为矩形，

∴AD∥BC，

∴∠B′HB=′DB′D′，

∴∠GHB′=∠EB′H，

∴GF∥B′E，

∵∠GB′H=∠B=90°，∠B′D′E=∠D=90°，

∴∠GB′H=∠B′D′E，

∴GB′∥EF，

∴四边形GB′EF为平行四边形；

（3）

解：如图2，

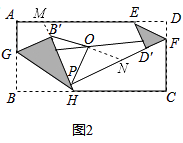
OB′=OP，理由是：

延长HB′交AD于M，延长B′O交D′P于点N，

∠B′HB=2∠GHB，∠DED′=2∠DEF，∠GHB=∠DEF，

∴∠B′HB=∠DED′，

∵AD∥BC，∠DMH=∠B′HB，

∴∠DED′=∠DMH，

∴ED′∥MH，

∴∠B′PN=∠ED′F=90°，

∴∠GB′P=∠B′PN，

∴GB′∥PD′，

∴∠B′GO=∠NFO，

∵∠GOB′=∠FON，GO=OF，

∴△GB′O≌△FNO，

∴B′O=NO，

∴B′O=OP．

【解析】解：（1）如图1，OB′=OD′，理由是：
连接OF，
由折叠得：∠GB′H=∠B=90°，∠B′D′E=∠D=90°，
∴∠GB′H=∠B′D′E，
∴GB′∥EF，
同理得B′E∥GF，
∴四边形GFEB′是平行四边形，
∴OB′=OF，
则B′、O、F共线，
在Rt△B′D′F中，OD′= B′F=OB′，
即OB′=OD′；
【考点精析】利用平行四边形的判定与性质对题目进行判断即可得到答案，需要熟知若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．