题目内容
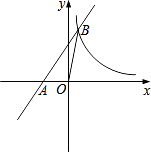
【题目】已知抛物线y=﹣x2+bx+c的图象经过点A(m,0)、B(0,n),其中m、n是方程x2﹣6x+5=0的两个实数根,且m<n.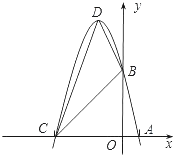
(1)求抛物线的解析式;
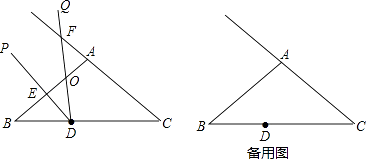
(2)设(1)中的抛物线与x轴的另一个交点为C,抛物线的顶点为D,求C、D点的坐标和△BCD的面积;
(3)P是线段OC上一点,过点P作PH⊥x轴,交抛物线于点H,若直线BC把△PCH分成面积相等的两部分,求P点的坐标.
【答案】
(1)
解:解方程x2﹣6x+5=0,
得x1=5,x2=1,
由m<n,知m=1,n=5,
∴A(1,0),B(0,5),
∴ ![]() ,即
,即 ![]() ;
;
所求抛物线的解析式为y=﹣x2﹣4x+5.
(2)
解:
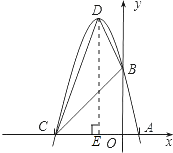
由﹣x2﹣4x+5=0,
得x1=﹣5,x2=1,
故C的坐标为(﹣5,0),
由顶点坐标公式,得D(﹣2,9);
过D作DE⊥x轴于E,得E(﹣2,0),
∴S△BCD=S△CDE+S梯形OBDE﹣S△OBC= ![]() =15.
=15.
(注:延长DB交x轴于F,由S△BCD=S△CFD﹣S△CFB也可求得)
(3)
解:设P(a,0),则H(a,﹣a2﹣4a+5);
直线BC把△PCH分成面积相等的两部分,须且只须BC等分线段PH,亦即PH的中点,
( ![]() )在直线BC上,
)在直线BC上,
易得直线BC方程为:y=x+5;
∴ ![]() .
.
解之得a1=﹣1,a2=﹣5(舍去),
故所求P点坐标为(﹣1,0).
【解析】(1)通过解方程可求出m、n的值,也就求出了点A、B的坐标,将它们代入抛物线的解析式中,通过联立方程组即可求得待定系数的值,从而确定该抛物线的解析式.(2)抛物线的解析式中,令y=0可求得C点坐标,利用公式法可求出抛物线顶点D的坐标;由于△BCD的面积无法直接求得,可过D作x轴的垂线,设垂足为E,分别求出△CDE、梯形DEOB、△BCO的面积,那么△CDE、梯形DEOB的面积和减去△BCO的面积,即可得到△BCD的面积.(3)若直线BC平分△PCH的面积,那么直线BC必过PH的中点,因为只有这样平分所得的两个三角形才等底等高,可设出点P的坐标,根据抛物线的解析式可表示出点H的坐标,进而可求得PH中点的坐标,由于PH中点在直线BC上,可将其代入直线BC的解析式中,由此求出点P的坐标.

【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.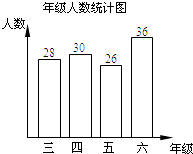
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
根据图表中提供的信息,回答下列问题:
(1)请将统计表补充完整
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
(2)测试学生中,成绩为80分的学生人数有 名;众数是 分;中位数是 分;
(3)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有 名.