Question

【题目】如图，正方形ABCD中，E是BD上一点，AE的延长线交CD于F，交BC的延长线于G，M是FG的中点，连接EC.

（1）求证：∠1=∠2；

（2）求证：．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

（1）根据正方形对角线平分一组对角线可得∠ADE=∠CDE，然后利用“边角边”证明△ADE和△CDE全等，根据全等三角形对应角相等可得∠1=∠2；

（2）根据直角三角形斜边上的中线等于斜边的一半可得MC=MF，再根据等边对等角可得∠MCF=∠MFC，然后求出∠2+∠MCF=90°，最后根据垂直的定义证明.

（1）证明：在正方形ABCD中，∠ADE=∠CDE，AD=CD，

在△ADE和△CDE中，

，

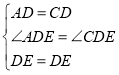∴△ADE≌△CDE(SAS)，

∴∠1=∠2；

（2）证明：∵M是FG的中点，

∴MC=MF，

∴∠MCF=∠MFC，

∵AD∥BC，

∴∠1=∠G，

∵∠G+∠MFC=90，

∴∠2+∠MCF=90,

∴EC⊥MC；