题目内容
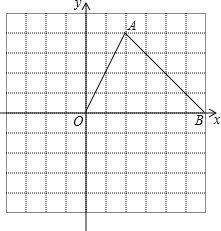
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
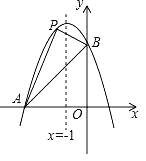
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
【答案】(1) y=﹣x2﹣2x+3;(2) 点Q(﹣1,![]() );(3) S△PAB有最大值
);(3) S△PAB有最大值![]() , 点P(﹣
, 点P(﹣![]() ,
,![]() )
)
【解析】
(1)抛物线经过两点![]() ,对称轴为直线
,对称轴为直线![]() ,则抛物线与
,则抛物线与![]() 轴另外一个交点坐标为:
轴另外一个交点坐标为:![]() ,即可求解;
,即可求解;
(2)设点![]() 是点
是点![]() 关于对称轴的对称点,则
关于对称轴的对称点,则![]() ,连接
,连接![]() 交对称轴于点
交对称轴于点![]() ,则点
,则点![]() 为所求,即可求解;
为所求,即可求解;
(3)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,由
,由![]() ,即可求解.
,即可求解.
解:(1)抛物线经过两点![]() ,对称轴为直线
,对称轴为直线![]() ,则抛物线与
,则抛物线与![]() 轴另外一个交点坐标为:
轴另外一个交点坐标为:![]() ,
,
则抛物线的表达式为:![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
个抛物线的表达式为:![]() ;
;
(2)设点![]() 是点
是点![]() 关于对称轴的对称点,则
关于对称轴的对称点,则![]() ,
,
连接![]() 交对称轴于点
交对称轴于点![]() ,则点
,则点![]() 为所求,
为所求,
则点![]() 的表达式为:
的表达式为:![]() ,
,
当![]() 时,
时,![]() ,故点
,故点![]() ;
;
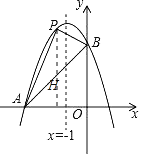
(3)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,
,
直线![]() 的表达式为:
的表达式为:![]() ,
,
设点![]() ,则点
,则点![]() ,
,
则![]() ,
,
![]()
![]() ,
,![]() 有最大值
有最大值![]() ,此时
,此时![]() ,
,
点![]() ,
,![]() .
.

练习册系列答案
相关题目