题目内容
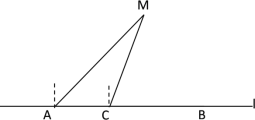
【题目】如图,在东西方向的海岸线l上有长为300米的码头AB,在码头的最西端A处测得轮船M在它的北偏东45°方向上;同一时刻,在A点正东方向距离100米的C处测得轮船M在北偏东22°方向上.
(1)求轮船M到海岸线l的距离;(结果精确到0.01米)
(2)如果轮船M沿着南偏东30°的方向航行,那么该轮船能否行至码头AB靠岸?请说明理由.
(参考数据:sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)
【答案】(1)167.79;(2)能.理由见解析.
【解析】
(1)过点M作MD⊥AC交AC的延长线于D,设DM=x.由三角函数表示出CD和AD的长,然后列出方程,解方程即可;
(2)作∠DMF=30°,交l于点F.利用解直角三角形求出DF的长度,然后得到AF的长度,与AB进行比较,即可得到答案.
解:(1)过点M作MD⊥AC交AC的延长线于D,设DM=x.
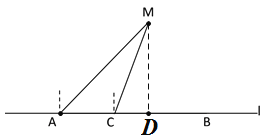
∵在Rt△CDM中,CD = DM·tan∠CMD= x·tan22°,
又∵在Rt△ADM中,∠MAC=45°,
∴AD=DM=x,
∵AD=AC+CD=100+ x·tan22°,
∴100+ x·tan22°=x.
∴![]() (米).
(米).
答:轮船M到海岸线l的距离约为167.79米.
(2)作∠DMF=30°,交l于点F.

在Rt△DMF中,有:
DF= DM·tan∠FMD= DM·tan30°=![]() DM≈
DM≈![]() ≈96.87米.
≈96.87米.
∴AF=AC+CD+DF=DM+DF≈167.79+96.87=264.66<300.
∴该轮船能行至码头靠岸.

练习册系列答案
相关题目