题目内容
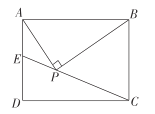
【题目】如图，由两个长为9，宽为3的全等矩形叠合而得到四边形ABCD，则四边形ABCD面积的最大值是_______.
【答案】15
【解析】
首先根据图1，证明四边形ABCD是菱形；然后判断出菱形的一条对角线为矩形的对角线时，四边形ABCD的面积最大，设AB=BC=x，则BE=9-x，利用勾股定理求出x的值，即可求出四边形ABCD面积的最大值是多少．
如图1，作AE⊥BC于E，AF⊥CD于F，
，
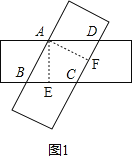∵AD∥BC，AB∥CD，
∴四边形ABCD是平行四边形，
∵两个矩形的宽都是3，
∴AE=AF=3，
∵S四边形ABCD=AEBC=AFCD，
∴BC=CD，
∴平行四边形ABCD是菱形．
如图2，
，
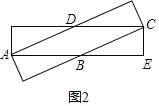设AB=BC=x，则BE=9-x，
∵BC2=BE2+CE2，
∴x2=（9-x）2+32，
解得x=5，
∴四边形ABCD面积的最大值是：
5×3=15．
故答案为：15.
练习册系列答案
相关题目
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … | -2 | -1 | 0 | 1 | 2 | … |
| … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知，下列说法中正确的是______.（填写序号）
①抛物线与轴的一个交点为
； ②函数的最大值为6；
③抛物线的对称轴是直线
； ④在对称轴左侧，随增大而增大.
