题目内容
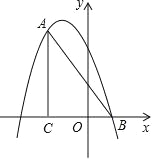
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2BO,AC=6,点B的坐标为(1,0),抛物线y=﹣x2+bx+c经过A、B两点.
(1)求点A的坐标;
(2)求抛物线的解析式;
(3)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE=![]() DE.
DE.
①求点P的坐标;
②在直线PD上是否存在点M,使△ABM为直角三角形?若存在,求出符合条件的所有点M的坐标;若不存在,请说明理由.
【答案】(1)y=﹣x2﹣3x+4;(2)①P(﹣1,6);②点M的坐标为:∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() )或(﹣1,﹣1)或(﹣1,
)或(﹣1,﹣1)或(﹣1,![]() ).
).
【解析】
(1)先根据已知求点A的坐标,利用待定系数法求二次函数的解析式;
(2)①先得AB的解析式为:y=-2x+2,根据PD⊥x轴,设P(x,-x2-3x+4),则E(x,-2x+2),根据PE=![]() DE,列方程可得P的坐标;
DE,列方程可得P的坐标;
②先设点M的坐标,根据两点距离公式可得AB,AM,BM的长,分三种情况:△ABM为直角三角形时,分别以A、B、M为直角顶点时,利用勾股定理列方程可得点M的坐标.
(1)∵B(1,0),
∴OB=1,
∵OC=2OB=2,
∴C(﹣2,0),
Rt△ABC中,tan∠ABC=2,
∴![]() =2,
=2,
∴![]() =2,
=2,
∴AC=6,
∴A(﹣2,6),
把A(﹣2,6)和B(1,0)代入y=﹣x2+bx+c得:![]() ,
,
解得:![]() ,
,
∴抛物线的解析式为:y=﹣x2﹣3x+4;
(2)①∵A(﹣2,6),B(1,0),
易得AB的解析式为:y=﹣2x+2,
设P(x,﹣x2﹣3x+4),则E(x,﹣2x+2),
∵PE=![]() DE,
DE,
∴﹣x2﹣3x+4﹣(﹣2x+2)=![]() (﹣2x+2),
(﹣2x+2),
x=1(舍)或﹣1,
∴P(﹣1,6);
②∵M在直线PD上,且P(﹣1,6),
设M(﹣1,y),
∴AM2=(﹣1+2)2+(y﹣6)2=1+(y﹣6)2,
BM2=(1+1)2+y2=4+y2,
AB2=(1+2)2+62=45,
分三种情况:
i)当∠AMB=90°时,有AM2+BM2=AB2,
∴1+(y﹣6)2+4+y2=45,
解得:y=3![]() ,
,
∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() );
);
ii)当∠ABM=90°时,有AB2+BM2=AM2,
∴45+4+y2=1+(y﹣6)2,y=﹣1,
∴M(﹣1,﹣1),
iii)当∠BAM=90°时,有AM2+AB2=BM2,
∴1+(y﹣6)2+45=4+y2,y=![]() ,
,
∴M(﹣1,![]() );
);
综上所述,点M的坐标为:∴M(﹣1,3+![]() )或(﹣1,3﹣
)或(﹣1,3﹣![]() )或(﹣1,﹣1)或(﹣1,
)或(﹣1,﹣1)或(﹣1,![]() ).
).

 阅读快车系列答案
阅读快车系列答案