Question

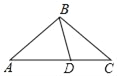
【题目】如图，在△ABC中，BA＝BC＝4，∠A＝30°，D是AC上一动点，

（Ⅰ）AC的长＝_____；

（Ⅱ）BD+DC的最小值是_____．

Answer 1

【答案】（Ⅰ）AC＝4 （Ⅱ）4，2.

【解析】

（Ⅰ）如图，过B作BE⊥AC于E，根据等腰三角形的性质和解直角三角形即可得到结论；

（Ⅱ）如图，作BC的垂直平分线交AC于D，则BD＝CD，此时BD+DC的值最小，解直角三角形即可得到结论．

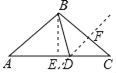
解：（Ⅰ）如图，过B作BE⊥AC于E，

∵BA＝BC＝4，

∴AE＝CE，

∵∠A＝30°，

∴AE＝AB＝2，

∴AC＝2AE＝4；

（Ⅱ）如图，作BC的垂直平分线交AC于D，

则BD＝CD，此时BD+DC的值最小，

∵BF＝CF＝2，

∴BD＝CD＝ ＝，

∴BD+DC的最小值＝2，

故答案为：4，2．