题目内容
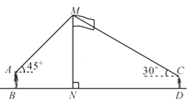
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)

【答案】①②③
【解析】
由AB=AC可知∠B=∠C,再由∠ADE=∠B可判断①;由三角形外角和定理可得∠ADB=∠DAC+∠C,∠DEC=∠DAC+∠ADE,而∠B=∠C=∠ADE=∠α,再由AB=AC且![]() 可求解出BC=16,则CD=16-6=10=AB,据此可判断②;由上问可知∠ADB=∠DEC,分∠DEC=90°和∠EDC=90°这两种情况进行求解即可判断③;若CD2=CECA,则
可求解出BC=16,则CD=16-6=10=AB,据此可判断②;由上问可知∠ADB=∠DEC,分∠DEC=90°和∠EDC=90°这两种情况进行求解即可判断③;若CD2=CECA,则![]() ,再由∠C是公共角,可得△ADE∽△ACD,而根据题干条件并不能得到该相似结论,据此可判断④.
,再由∠C是公共角,可得△ADE∽△ACD,而根据题干条件并不能得到该相似结论,据此可判断④.
解:由AB=AC可知∠B=∠C,再由∠ADE=∠B可知△ADE∽△ACD,故①正确;由三角形外角和定理可得∠ADB=∠DAC+∠C,∠DEC=∠DAC+∠ADE,而∠B=∠C=∠ADE,故∠ADB=∠DEC.由AB=AC=10且![]() ,可求解BC=16,则CD=16-6=10=AB.综合上述,由∠B=∠C、∠ADB=∠DEC、CD=AB可证明△ABD≌△DCE;由上问可知∠ADB=∠DEC,当∠DEC=90°时,∠ADB=90°,则D点为BC中点,BD=8.当∠EDC=90°时,则∠BAD=90°,则BD=
,可求解BC=16,则CD=16-6=10=AB.综合上述,由∠B=∠C、∠ADB=∠DEC、CD=AB可证明△ABD≌△DCE;由上问可知∠ADB=∠DEC,当∠DEC=90°时,∠ADB=90°,则D点为BC中点,BD=8.当∠EDC=90°时,则∠BAD=90°,则BD=![]() ,故③正确;若CD2=CECA,则
,故③正确;若CD2=CECA,则![]() ,再由∠C是公共角,可得△ADE∽△ACD,而根据题干条件并不能得到该相似结论,故④错误;
,再由∠C是公共角,可得△ADE∽△ACD,而根据题干条件并不能得到该相似结论,故④错误;
故答案为:①②③.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案【题目】某校八年级甲.乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:
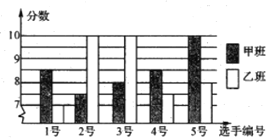
(1)根据上图求出下表所缺数据:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题
(1)当x=3时,y=
(2)当x为何值时,y=0?
(3)①若自变量x的取值范围是0≤x≤5,求函数值y的取值范围;
②若函数值y为正数,则自变量x的取值范围.