题目内容
【题目】如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E（点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．
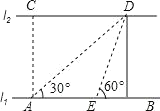
【答案】C、D两点间的距离为30m.
【解析】直接利用等腰三角形的判定与性质得出DE=AE=20，进而求出EF的长，再得出四边形ACDF为矩形，则CD=AF=AE+EF求出答案．
解：过点D作l1的垂线，垂足为F，
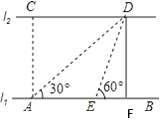
∵∠DEB=60°，∠DAB=30°，
∴∠ADE=∠DEB﹣∠DAB=30°，
∴△ADE为等腰三角形，
∴DE=AE=20，
在Rt△DEF中，EF=DEcos60°=20×
=10，
∵DF⊥AF，
∴∠DFB=90°，
∴AC∥DF，由已知l1∥l2，
∴CD∥AF，
∴四边形ACDF为矩形，CD=AF=AE+EF=30，
答：C、D两点间的距离为30m
“点睛”此题考查了两点之间的距离以及等腰三角形的判定与性质以及锐角三角函数关系，得出EF的长是解题关键.
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
