题目内容
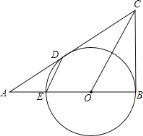
【题目】若![]() 的弦
的弦![]() 与
与![]() 的半径之比为
的半径之比为![]() ,则弦
,则弦![]() 所对的圆周角等于________.
所对的圆周角等于________.
【答案】![]() 或
或![]()
【解析】
作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,根据垂径定理得AC=BC,由于AB:OA=![]() :1,则AC:OA=
:1,则AC:OA=![]() :2,在Rt△OAC中,根据余弦的定义可求出∠OAC=30°,则∠AOB=120°,然后根据圆周角定理得到∠APB=
:2,在Rt△OAC中,根据余弦的定义可求出∠OAC=30°,则∠AOB=120°,然后根据圆周角定理得到∠APB=![]() ∠AOB=60°,根据圆内接四边形的性质得到∠ADB=180°-∠APB=120°.
∠AOB=60°,根据圆内接四边形的性质得到∠ADB=180°-∠APB=120°.
作OC⊥AB于C,∠APB和∠ADB为弦AB所对的圆周角,
∵OC⊥AB,
∴AC=BC,
∵AB:OA=![]() :1,
:1,
∴AC:OA=![]() :2,
:2,
在Rt△OAC中,cos∠OAC=![]() ,
,
∴∠OAC=30°,
而OA=OB,
∴∠OBA=30°,
∴∠AOB=120°,
∴∠APB=![]() ∠AOB=60°,
∠AOB=60°,
∴∠ADB=180°-∠APB=120°,
即弦AB所对的圆周角等于60°或120°.
故答案为60°或120°.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目