题目内容
【题目】如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF.你认为( )
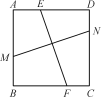
A. 仅小明对 B. 仅小亮对 C. 两人都对 D. 两人都不对
【答案】C
【解析】
分别过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,设EF与MN相交于点O,MP与EF相交于点Q,根据正方形的性质可得EG=MP;对于小明的说法,先利用“HL”证明Rt△EFG≌Rt△MNP,根据全等三角形对应角相等可得∠MNP=∠EFG,再根据角的关系推出∠EQM=∠MNP,然后根据∠MNP+∠NMP=90°得到∠NMP+∠EQM=90°,从而得到∠MOQ=90°,根据垂直的定义即可证得MN⊥EF;对于小亮的说法,先推出∠EQM=∠EFG,∠EQM=∠MNP,然后得到∠EFG=∠MNP,然后利用“角角边”证明△EFG≌△MNP,根据全等三角形对应边相等可得EF=MN.
如图,过点E作EG⊥BC于点G,过点M作MP⊥CD于点P,设EF与MN相交于点O,MP与EF相交于点Q,
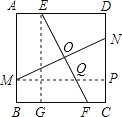
∵四边形ABCD是正方形,
∴EG=MP,
对于小明的说法:
在Rt△EFG和Rt△MNP中,
![]() ,
,
∴Rt△EFG≌Rt△MNP(HL),
∴∠MNP=∠EFG,
∵MP⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG=∠MNP,
又∵∠MNP+∠NMP=90°,
∴∠EQM+∠NMP=90°,
在△MOQ中,∠MOQ=180°-(∠EQM+∠NMP)=180°-90°=90°,
∴MN⊥EF,
故甲正确.
对小亮的说法:
∵MP⊥CD,∠C=90°,
∴MP∥BC,
∴∠EQM=∠EFG,
∵MN⊥EF,
∴∠NMP+∠EQM=90°,
又∵MP⊥CD,
∴∠NMP+∠MNP=90°,
∴∠EQM=∠MNP,
∴∠EFG=∠MNP,
在△EFG和△MNP中,
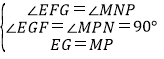 ,
,
∴△EFG≌△MNP(AAS),
∴MN=EF,故小亮的说法正确,
综上所述,两个人的说法都正确.
故选C.