题目内容
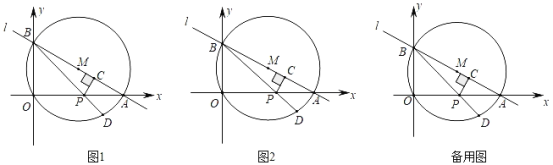
【题目】如图1,直线l:y=﹣![]() x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
x+4与x轴交于点A,与y轴交于点B,以AB为直径作⊙M,点P为线段OA上一动点(与点O、A不重合),作PC⊥AB于C,连结BP并延长交⊙O于点D.
(1)求点A,B的坐标和tan∠BAO的值;
(2)设![]() =x,tan∠BPO=y.
=x,tan∠BPO=y.
①当x=1时,求y的值及点D的坐标;
②求y关于x的函数表达式;
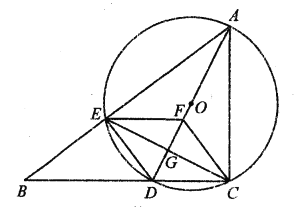
(3)如图2,连接OC,当点P在线段OA上运动时,求OCPD的最大值.
【答案】(1)点A、B的坐标分别为:(8,0)、(0,4);![]() ;(2)①y=
;(2)①y=![]() ,点D的坐标为(
,点D的坐标为(![]() ,﹣
,﹣![]() );②y=
);②y=![]() ;(3)当x=4时,OCPD最大值为
;(3)当x=4时,OCPD最大值为![]()
【解析】
(1)对于直线l:y=﹣![]() x+4,令x=0,则y=4,令y=0,则x=8,求出点A、B的坐标,即可求解;
x+4,令x=0,则y=4,令y=0,则x=8,求出点A、B的坐标,即可求解;
(2)①当x=1时,则BC=AC,PB=PA=![]() ,进而确定直线BP的表达式;根据DM是圆的半径,即可求出点D的坐标;
,进而确定直线BP的表达式;根据DM是圆的半径,即可求出点D的坐标;
②AB=AC+BC,求得PA=![]() ,即可求解;
,即可求解;
(3)证明△OAC∽△ODP,利用二次函数求最大值的方法,即可求解.
解:(1)对于直线l:y=﹣![]() x+4,令x=0,则y=4,令y=0,则x=8,
x+4,令x=0,则y=4,令y=0,则x=8,
故点A、B的坐标分别为:(8,0)、(0,4);
∴tan∠BAO=![]() =
=![]() =
=![]() ;
;
(2)由点A、B的坐标得:AB=![]() =4
=4![]() ,则圆的半径r=2
,则圆的半径r=2![]() ,
,
①如图1,当x=1时,则BC=AC,

又∵PM⊥AB,
∴AM=BM=![]() AB=2/span>
AB=2/span>![]() ,
,
∵tan∠BAO=![]() =
=![]() =
=![]() ,则cos∠BAO=
,则cos∠BAO=![]() ,
,
PB=PA=![]() =
=![]() =5,
=5,
OP=OA﹣AP=8﹣5=3,故点P(3,0),
在Rt△BOP中,y=tan∠BPO=![]() =
=![]() ;
;
设直线BP的表达式为:y=kx+b,则![]() ,解得:
,解得: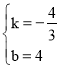 ,
,
故直线BP的表达式为:y=﹣![]() x+4,
x+4,
设点D的坐标为:(m,﹣![]() m+4),
m+4),
∵点M是AB的中点,则其坐标为:(4,2),
∵DM是圆的半径,
∴MD=(m﹣4)2+(﹣![]() m+4﹣2)2=(2
m+4﹣2)2=(2![]() )2,
)2,
解得:m=0或![]() (舍去0),
(舍去0),
故m=![]() ,
,
故点D(![]() ,﹣
,﹣![]() );
);
故y=![]() ,点D的坐标为(
,点D的坐标为(![]() ,﹣
,﹣![]() );
);
②在△Rt△ACP中,AC=![]() =
=![]() PA,
PA,
∵![]() =x,则BC=xAC,
=x,则BC=xAC,
∵AB=AC+BC=![]() PA+
PA+![]() PAx=4
PAx=4![]() ,
,
∴PA=![]() ,
,
∵OP=OA﹣PA=4﹣![]() ,
,
y=tan∠BPO=![]() =
=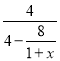 =
=![]() ;
;
(3)如图2,连接OD、OC,
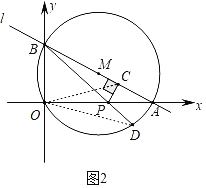
∵∠BOA=90°,∠BCP=90°,
∴O、P、C、B四点共圆,
∴∠COP=∠CBP,
而∠CBP=∠AOD,
∴∠COP=∠AOD,
而∠BDO=∠BAO,
∴△OAC∽△ODP,
∴![]() ,即OCPD=ACOP,
,即OCPD=ACOP,
设PA=x,则OP=8﹣x,
在Rt△ACP中,AC=APcos∠BAO=![]() x=
x=![]() x,
x,
∴OCPD=ACOP=![]() x(8﹣x)=﹣
x(8﹣x)=﹣![]() x2+
x2+![]() x,
x,
∵﹣![]() <0,故OCPD有最大值,
<0,故OCPD有最大值,
当x=4时,OCPD最大值为![]() .
.

 一本好题口算题卡系列答案
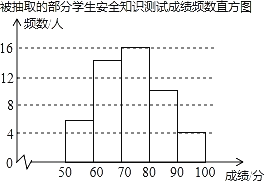
一本好题口算题卡系列答案【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.