题目内容
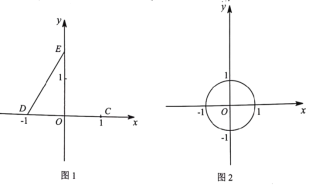
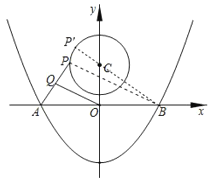
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,![]() 是以点
是以点![]() 为圆心,2为半径的圆上的动点,
为圆心,2为半径的圆上的动点,![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() .则线段
.则线段![]() 的最大值是________.
的最大值是________.

【答案】3.5
【解析】
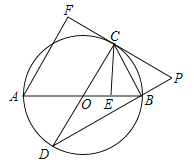
连接BP,如图,先解方程![]() =0得A(4,0),B(4,0),再判断OQ为△ABP的中位线得到OQ=
=0得A(4,0),B(4,0),再判断OQ为△ABP的中位线得到OQ=![]() BP,利用点与圆的位置关系,BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,然后计算出BP′即可得到线段OQ的最大值.
BP,利用点与圆的位置关系,BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,然后计算出BP′即可得到线段OQ的最大值.
连接BP,如图,
当y=0时,![]() =0,
=0,
解得x1=4,x2=4,则A(4,0),B(4,0),
∵Q是线段PA的中点,
∴OQ为△ABP的中位线,
∴OQ=![]() BP,
BP,
当BP最大时,OQ最大,
而BP过圆心C时,PB最大,如图,点P运动到P′位置时,BP最大,
∵BC=![]() ∴BP′=5+2=7,
∴BP′=5+2=7,
∴线段OQ的最大值是3.5,
故答案为:3.5.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目