题目内容
【题目】五一期间，乐乐与小佳两个人打算骑共享单车骑行出游，两人打开手机
进行选择，已知附近共有3种品牌的4辆车，其中
品牌有2辆，
品牌和
品牌各有1辆，手机上无法识别品牌，且有人选中车后其他人无法再选．
（1）若乐乐首先选择，求乐乐选中品牌单车的概率；
（2）请用画树状图或列表的方法求乐乐和小佳选中同一品牌单车的概率．
【答案】（1）
；（2）
．
【解析】
（1）直接用概率公式即可.
（2）先列出所有的可能结果，注意两个人不能选择同一辆车，再找出两个人选择同一品牌所占的结果数，最后用概率公式即可.
解：（1）若乐乐首先选择，则乐乐选中
品牌单车的概率为；
（2）列表如下：（记
品牌2辆车为：
，
）
|
|
|
| |
| — |
|
|
|
|
| — |
|
|
|
|
| — |
|
|
|
|
| — |
由表可知，共有12种等可能的结果，其中两人选中同一品牌单车有2种；
∴所求概率为
．
课课优能力培优100分系列答案
优百分课时互动系列答案
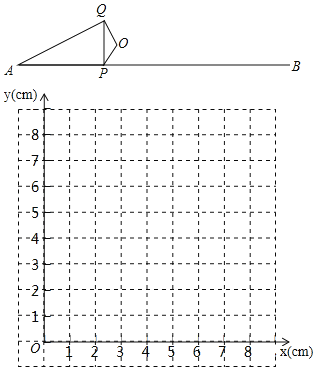
【题目】如图，P是线段AB上的一点，AB＝6cm，O是AB外一定点．连接OP，将OP绕点O顺时针旋转120°得OQ，连接PQ，AQ．小明根据学习函数的经验，对线段AP，PQ，AQ的长度之间的关系进行了探究．
下面是小明的探究过程，请补充完整：
（1）对于点P在AB上的不同位置，画图、测量，得到了线段AP，PQ，AQ的长度（单位：cm）的几组值，如表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP，PQ，AQ的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；/span>
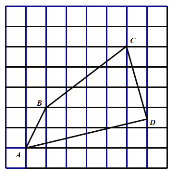
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当AQ＝PQ时，线段AP的长度约为 cm．
