题目内容
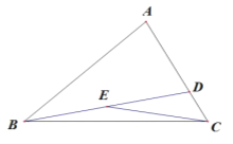
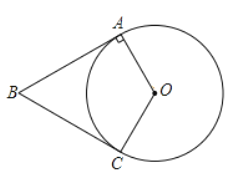
【题目】如图,四边形OABC中,![]() .OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
.OA=OC, BA=BC.以O为圆心,以OA为半径作☉O
(1)求证:BC是☉O的切线:
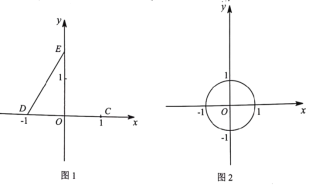
(2)连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与此的延长线交于点F若![]() .
.
①补全图形;
②求证:OF=OB.
【答案】(1)证明见解析(2)①图见解析(2)证明见解析
【解析】
(1)连接AC,根据等腰三角形的性质得到∠OAC=∠OCA,∠BAC=∠BCA,得到∠OCB=∠OAB=90°,根据切线的判定定理证明;
(2)①根据题意画出图形;
②根据切线长定理得到BA=BC,得到BD是AC的垂直平分线,根据垂径定理、圆心角和弧的关系定理得到∠AOC=120°,根据等腰三角形的判定定理证明结论.
(1)证明:如图1,连接AC,
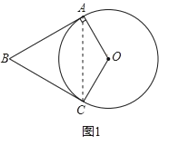
∵OA=OC,
∴∠OAC=∠OCA,
∵BA=BC,
∴∠BAC=∠BCA,
∴∠OAC+∠BCA=∠OCA+∠BCA,即∠OCB=∠OAB=90°,
∴OC⊥BC,
∴BC是⊙O的切线;
(2)①解:补全图形如图2;
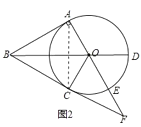
②证明:∵∠OAB=90°,
∴BA是⊙O的切线,又BC是⊙O的切线,
∴BA=BC,
∵BA=BC,OA=OC,
∴BD是AC的垂直平分线,
∴![]() ,
,
∵![]() ,
,
∴![]() =
=![]() ,
,
∴∠AOC=120°,
∴∠AOB=∠COB=∠COE=60°,
∴∠OBF=∠F=30°,
∴OF=OB.

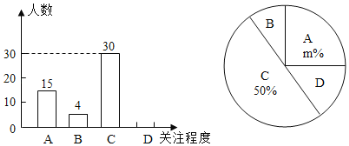
【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
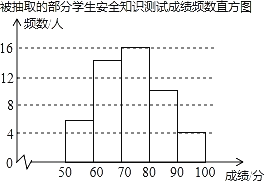
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.