题目内容
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,得到
所在的直线翻折,得到![]() ,连接
,连接![]() .
.
(1)点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
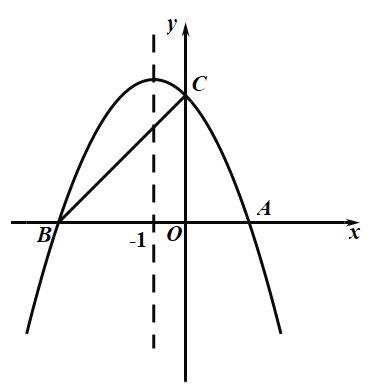
(2)如图1,若点![]() 落在抛物线的对称轴上,且在
落在抛物线的对称轴上,且在![]() 轴上方,求抛物线的解析式.
轴上方,求抛物线的解析式.
(3)设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)A(-1,0),B(3,0);(2)![]() ;(3)
;(3)![]() 或m=
或m=![]()
【解析】
(1)令![]() =0,求出x的值,即可求解;
=0,求出x的值,即可求解;
(2)过点B作y轴的平行线BQ,过点D作x轴的平行线交y轴于点P、交BQ于点Q,证明△CPD∽△DQB,则![]() ,代入即可求解;
,代入即可求解;
(3)连接OD交BC于点H,则DO⊥BC,过点H、D分别作x轴的垂线交于点N、M,用含m的式子表示S1,S2,根据![]() 得到DM=-
得到DM=-![]() m,进而表示出HN=
m,进而表示出HN=![]() DM=-
DM=-![]() m根据OC∥HN得到△BOC∽△BNH,得到
m根据OC∥HN得到△BOC∽△BNH,得到![]() ,求出BN,ON,根据垂直关系得到∠BHN=∠HON,由正切的定义可知
,求出BN,ON,根据垂直关系得到∠BHN=∠HON,由正切的定义可知![]() ,从而得到关于m的方程,故可求解.
,从而得到关于m的方程,故可求解.
(1)令![]() =0,
=0,
解得x1=-1,x2=3
∴A(-1,0),B(3,0)
故答案为:(-1,0);(3,0);
(2)过点B作y轴的平行线BQ,过点D作x轴的平行线交y轴于点P、交BQ于点Q,
∵∠CDP+∠DCP=90°,∠PDC+∠QDB=90°,
∴∠QDB=∠DCP,
∵对称轴x=-![]() ,
,
设:D(1,n)(n>0),点C(0,3m),
∵∠CPD=∠BQD=90°,
∴△CPD∽△DQB,
∴![]() ,
,
其中:CP=n+3m,DQ=31=2,PD=1,BQ=n,CD=CO=3m,BD=OB=3,
将以上数值代入比例式得![]()
故抛物线的表达式为:![]() ;
;

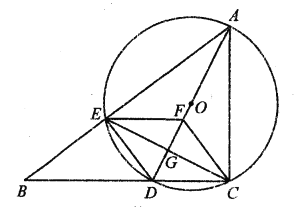
(3)如图2,连接OD交BC于点H,则DO⊥BC,过点H、D分别作x轴的垂线交于点N、M,
∵OC=3m,
S1=S△OBD=![]() ×OB×DM=
×OB×DM=![]() DM,
DM,
S2=S△OAC=![]() ×AO×OC=-
×AO×OC=-![]() m,而
m,而![]() ,
,
则DM=-![]() m,
m,
∵H是OD的中点,∴HN=![]() DM=-
DM=-![]() m=
m=![]() OC,
OC,
∵OC∥HN
∴△BOC∽△BNH
∴![]()
∴BN=![]() BO=
BO=![]() ,则ON=3
,则ON=3![]() =
=![]() ,
,
则DO⊥BC,HN⊥OB,
∴∠HON+∠HBO=90°,∠BHN+∠HBO=90°,
则∠BHN=∠HON,则tan∠BHN=tan∠HON,
则![]()
∴HN2=ON×BN=![]() =(-
=(-![]() m
m
解得:m=±![]() .
.
∴![]() 或m=
或m=![]() .
.


 寒假乐园北京教育出版社系列答案
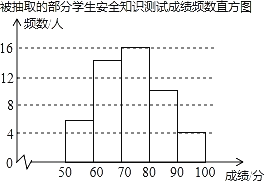
寒假乐园北京教育出版社系列答案【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.
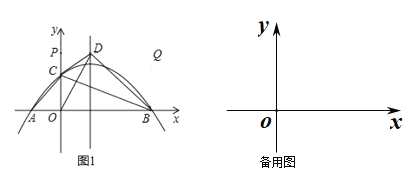
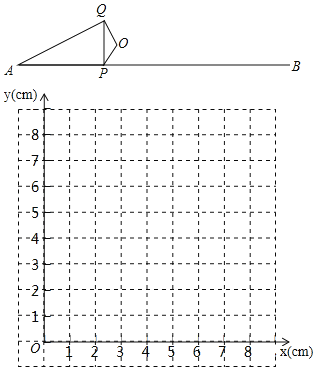
【题目】如图,P是线段AB上的一点,AB=6cm,O是AB外一定点.连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ.小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;/span>
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为 cm.
【题目】某班甲、乙、丙三名同学20天的体温数据记录如下表:
甲的体温 | 乙的体温 | 丙的体温 | ||||||||||||
温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 | 温度(℃) | 36.1 | 36.4 | 36.5 | 36.8 |
频数 | 5 | 5 | 5 | 5 | 频数 | 6 | 4 | 4 | 6 | 频数 | 4 | 6 | 6 | 4 |
则在这20天中,甲、乙、丙三名同学的体温情况最稳定的是________.