题目内容
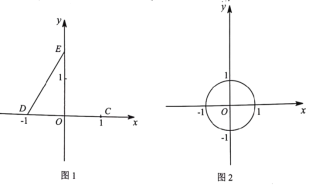
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,交
,交![]() 轴于点
轴于点![]() 的长为
的长为![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是第一象限抛物线上的一点,直线
是第一象限抛物线上的一点,直线![]() 交
交![]() 轴于
轴于![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() 的长为
的长为![]() ,用含
,用含![]() 的式子表示
的式子表示![]() ;
;
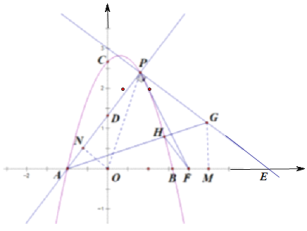
(3)在![]() 的条件下,过点
的条件下,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 在
在![]() 轴上,
轴上,![]() ,连接
,连接![]()
![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1) ![]() ; (2)
; (2) ![]() ;(3)
;(3) ![]()
【解析】
(1)根据题意可得抛物线对称轴为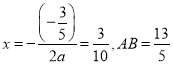 ,得到A点坐标,进而可得抛物线解析式;
,得到A点坐标,进而可得抛物线解析式;
(2)作PQ⊥x轴于点Q,易证![]() ,利用相似三角形的性质可得OD关于t的式子,进而得到答案;
,利用相似三角形的性质可得OD关于t的式子,进而得到答案;
(3)设![]() ,整理可得
,整理可得![]() ,则
,则![]() ,解得可证
,解得可证![]() ,则
,则![]() ,进而得到
,进而得到![]() ,即
,即![]() ,设
,设![]() ,
,![]() ,在R
,在R![]() 中根据勾股定理求得m=2,作
中根据勾股定理求得m=2,作![]() 于点
于点![]() ,再利用三角形正切函数求得相关线段长,然后即可得到G点坐标.
,再利用三角形正切函数求得相关线段长,然后即可得到G点坐标.
解:![]() 抛物线的对称轴为
抛物线的对称轴为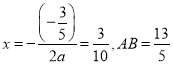 ,
,
![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() ,
,
把![]() 坐标代抛物线可得,
坐标代抛物线可得,
![]() ;
;
如图,作PQ⊥x轴于点Q,
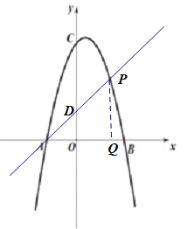
易证![]() ,
,
![]() ,
,
∴![]()
![]()
![]() ,
,
![]() ;
;
![]() 设
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
在R![]() 中根据勾股定理
中根据勾股定理![]() ,
,
![]() ,
,
解得![]() ,
,
作![]() 于点
于点![]() ,
,
tan![]() ,
,
设![]() ,
,
![]() ,
,
∴tan![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,![]() ,
,
![]()

 心算口算巧算一课一练系列答案
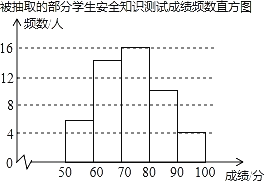
心算口算巧算一课一练系列答案【题目】某校为了解学生对“防溺水”安全知识的掌握情况,从全校1500名学生中随机抽取部分学生进行测试,并将测试成绩(百分制,得分均为整数)进行统计分析,绘制了不完整的频数表和频数直方图.
组别 | 成绩x(分) | 频数(人) | 频率 |
A组 | 50≤x<60 | 6 | 0.12 |
B组 | 60≤x<70 | a | 0.28 |
C组 | 70≤x<80 | 16 | 0.32 |
D组 | 80≤x<90 | 10 | 0.20 |
E组 | 90≤x≤100 | 4 | 0.08 |
由图表中给出的信息回答下列问题:
(1)表中的a= ;抽取部分学生的成绩的中位数在 组;
(2)把如图的频数直方图补充完整;
(3)如果成绩达到80分以上(包括80分)为优秀,请估计该校1500名学生中成绩优秀的人数.
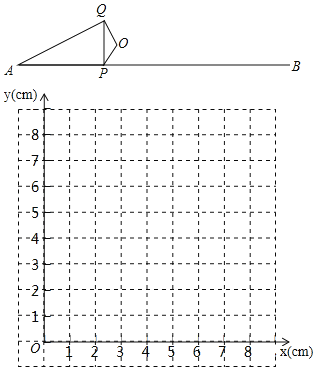
【题目】如图,P是线段AB上的一点,AB=6cm,O是AB外一定点.连接OP,将OP绕点O顺时针旋转120°得OQ,连接PQ,AQ.小明根据学习函数的经验,对线段AP,PQ,AQ的长度之间的关系进行了探究.
下面是小明的探究过程,请补充完整:
(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,PQ,AQ的长度(单位:cm)的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
AP | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PQ | 4.00 | 2.31 | 0.84 | 1.43 | 3.07 | 4.77 | 6.49 |
AQ | 4.00 | 3.08 | 2.23 | 1.57 | 1.40 | 1.85 | 2.63 |
在AP,PQ,AQ的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;/span>
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解决问题:当AQ=PQ时,线段AP的长度约为 cm.