题目内容
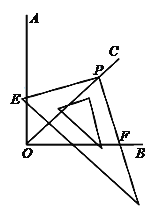
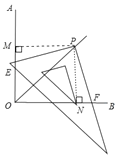
【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。
【答案】答案见解析
【解析】试题分析:过点P作PM⊥OA于M,PN⊥OB于N,就可以得出PM=PN,四边形PMON是矩形,就可以得出∠MPN=90°,可以求出∠MPE=∠NPF,证△MPE≌△NPF就可以得出结论.
证明:过点P作PM⊥OA于M,PN⊥OB于N.
又∵P为∠AOB的平分线OC上的任意一点,
∴PM=PN.又知∠MPN=∠EPF=90°,
∴∠MPN-∠EPN=∠EPF-∠EPN
∴∠EPM=∠FPN,在△PME与△PNF中,
∠EPM=∠FPN,PM=PN。∠EMP=∠FNP,
∴△PME≌△PNF(ASA),
∴PE=PF。

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目