题目内容
【题目】(1)问题解决:如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
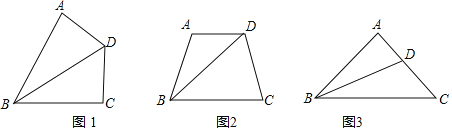
①如图1,若α=90°,根据教材中一个重要性质直接可得AD=CD,这个性质是 ;
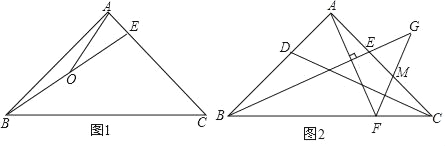
②在图2中,求证:AD=CD;
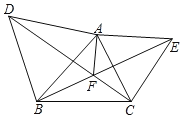
(2)拓展探究:根据(1)的解题经验,请解决如下问题:如图3,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证BD+AD=BC.
【答案】(1)①角平分线上的点到角的两边距离相等;②见解析;(2)见解析.
【解析】
(1)①根据角平分线的性质定理即可解决问题;
②如图2中,作DE⊥BA于E,DF⊥BC于F.只要证明△DEA≌△DFC即可解决问题;
(2)如图3中,在BC时截取BK=BD,BT=BA,连接DK.首先证明DK=CK,再证明△DBA≌△DBT,推出AD=DT,∠A=∠BTD=100°,推出∠DTK=∠DKT=80°,推出DT=DK=CK,由此即可解决问题;
(1)①根据角平分线的性质定理可知AD=CD.
所以这个性质是角平分线上的点到角的两边距离相等.
故答案为:角平分线上的点到角的两边距离相等.
②如图2中,作DE⊥BA于E,DF⊥BC于F.
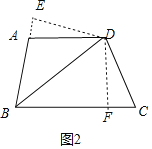
∵BD平分∠EBF,DE⊥BE,DF⊥BF,
∴DE=DF,
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,
∴∠EAD=∠C,
∵∠E=∠DFC=90°,
∴△DEA≌△DFC,
∴DA=DC.
(2)如图3中,在BC上截取BK=BD,BT=BA,连接DK.
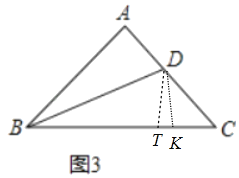
∵AB=AC,∠A=100°,
∴∠ABC=∠C=40°,
∵BD平分∠ABC,
∴∠DBK=![]() ∠ABC=20°,
∠ABC=20°,
∵BD=BK,
∴∠BKD=∠BDK=80°,
∵∠BKD=∠C+∠KDC,
∴∠KDC=∠C=40°,
∴DK=CK,
∵BD=BD,BA=BT,∠DBA=∠DBT,
∴△DBA≌△DBT,
∴AD=DT,∠A=∠BTD=100°,
∴∠DTK=∠DKT=80°,
∴DT=DK=CK,
∴BD+AD=BK+CK=BC.

 名校课堂系列答案
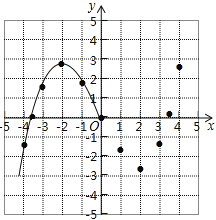
名校课堂系列答案【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.