题目内容
【题目】综合与实践:
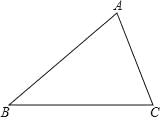
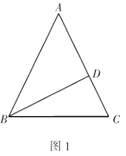
如图1,![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,
,![]() 且
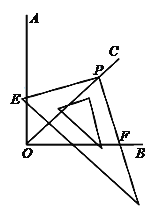
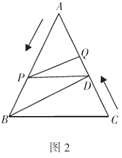
且![]() ;如图2,在图1的基础上,动点
;如图2,在图1的基础上,动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 的速度沿线段
的速度沿线段![]() 向点
向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发以相同速度沿线段
出发以相同速度沿线段![]() 向点
向点![]() 运动,当其中一点到达终点时另外一点也随之停止运动,设点
运动,当其中一点到达终点时另外一点也随之停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 的长;
的长;
(2)当![]() 的其中一边与
的其中一边与![]() 平行时(
平行时(![]() 与
与![]() 不重合),求
不重合),求![]() 的值;
的值;
(3)点![]() 在线段
在线段![]() 上运动的过程中,是否存在以
上运动的过程中,是否存在以![]() 为腰的
为腰的![]() 是等腰三角形?若存在,求出
是等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 的值为2.5秒或3秒;(3)存在,
的值为2.5秒或3秒;(3)存在,![]() 的值为3或
的值为3或![]() 秒.
秒.
【解析】
(1)设![]() ,
,![]() ,则
,则![]() ,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
,在Rt△ABD中利用勾股定理建立方程求出x,即可得到AB的长;
(2)分两种情况讨论:①当![]() 时,
时,![]() ;②当
;②当![]() 时,
时,![]() ,分别建立方程求解;
,分别建立方程求解;
(3)分两种情况讨论:①当![]() 时,易得
时,易得![]() ;②当
;②当![]() 时,过点
时,过点![]() 作
作![]() 于点
于点![]() ,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
,利用等积法求出DE,再用勾股定理求出AE,进而得到AP,用距离除以速度即可得出时间.
解:(1)设![]() ,
,![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
∴![]() .
.
(2)由(1)可得:![]() ,
,![]() ,
,![]() ,
,
∵动点![]() 、
、![]() 以每秒
以每秒![]() 的速度运动,时间为
的速度运动,时间为![]() ,
,
∴![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() ;
;
②当![]() 时,
时,![]() ,
,
即![]() ,
,
∴![]() .
.
∴当![]() 的其中一边与
的其中一边与![]() 平行时,
平行时,![]() 的值为2.5秒或3秒.
的值为2.5秒或3秒.
(3)存在,分两种情况讨论:
①如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
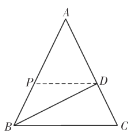
∴![]() ,
,
∴![]() ,
,
②如图,当![]() 时,
时,![]() 是等腰三角形.
是等腰三角形.
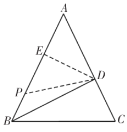
过点![]() 作
作![]() 于点
于点![]() ,
,
在![]() 中,
中,![]() ,
,
即:![]() ,
,
∴![]() ,
,
在![]() 中,
中,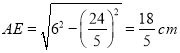 .
.
∴![]() ,
,
∴![]() .
.
综上,当![]() 的值为3或
的值为3或![]() 秒时,
秒时,![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目