题目内容
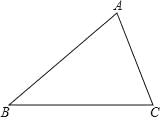
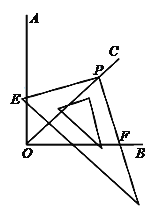
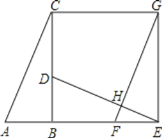
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
【答案】(1)FG⊥ED,理由详见解析;(2)详见解析
【解析】
(1)由旋转及平移的性质可得到∠DEB+∠GFE=90°,可得出结论;
(2)由旋转和平移的性质可得BE=CB,CG∥BE,从而可证明四边形CBEG是矩形,再结合CB=BE可证明四边形CBEG是正方形.
(1)FG⊥ED.
理由如下:
∵△ABC绕点B顺时针旋转90°至△DBE后,
∴∠DEB=∠ACB,
∵把△ABC沿射线平移至△FEG,
∴∠GFE=∠A,
∵∠ABC=90°,
∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°,
∴∠FHE=90°,
∴FG⊥ED;
(2)根据旋转和平移可得∠GEF=90°,∠CBE=90°,CG∥EB,CB=BE,
∵CG∥EB,
∴∠BCG=∠CBE=90°,
∴∠BCG=90°,
∴四边形BCGE是矩形,
∵CB=BE,
∴四边形CBEG是正方形.

练习册系列答案
相关题目
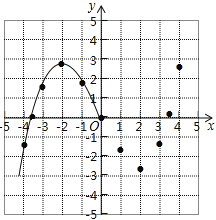
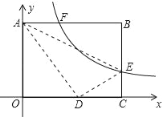
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.