ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌ![]() гы
гы![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
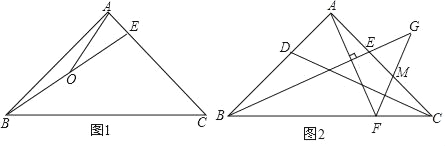
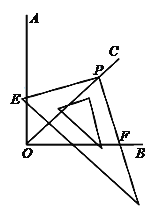
ЃЈ1ЃЉШчЭМ1ЃЌЕу![]() дк
дк![]() ЩЯЃЌЕу
ЩЯЃЌЕу![]() гы
гы![]() жиКЯЃЌ
жиКЯЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌдђЯпЖЮ
ЕФжаЕуЃЌдђЯпЖЮ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ ЃЌ
ЕФЪ§СПЙиЯЕЪЧ ЃЌ![]() гы
гы![]() ЕФЮЛжУЪЧ ЃЎ
ЕФЮЛжУЪЧ ЃЎ
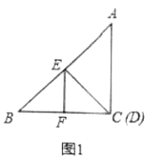
ЃЈ2ЃЉШчЭМ2ЃЌдкЭМ1ЕФЛљДЁЩЯЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЕНШчЭМ2ЕФЮЛжУЃЌЦфжа
ЫГЪБеыа§зЊЕНШчЭМ2ЕФЮЛжУЃЌЦфжа![]() дквЛЬѕжБЯпЩЯЃЌ
дквЛЬѕжБЯпЩЯЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌдђЯпЖЮ
ЕФжаЕуЃЌдђЯпЖЮ![]() гы
гы![]() ЪЧЗёДцдкФГжжШЗЖЈЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПжЄУїФуЕФНсТлЃЎ
ЪЧЗёДцдкФГжжШЗЖЈЕФЪ§СПЙиЯЕКЭЮЛжУЙиЯЕЃПжЄУїФуЕФНсТлЃЎ
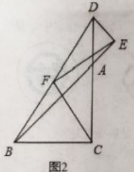
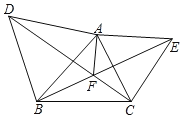
ЃЈ3ЃЉШє![]() ШЦ
ШЦ![]() Еуа§зЊШЮвтвЛИіНЧЖШЕНШчЭМ3ЕФЮЛжУЃЌ
Еуа§зЊШЮвтвЛИіНЧЖШЕНШчЭМ3ЕФЮЛжУЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌЧыФуЭъГЩЭМ3ЃЌВТЯыЯпЖЮ
ЃЌЧыФуЭъГЩЭМ3ЃЌВТЯыЯпЖЮ![]() гы
гы![]() ЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉEF=FCЃЌEFЁЭFCЃЛЃЈ2ЃЉEF=FCЃЌEFЁЭFCЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉEF=FCЃЌEFЁЭFCЃЌжЄУїМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЕУГіЁїEFCЪЧЕШбќжБНЧШ§НЧаЮМДПЩЃЎ
ЃЈ2ЃЉбгГЄЯпЖЮCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂECЃЌРћгУSASжЄЁїBFCЁеЁїDFMЃЌНјЖјПЩвджЄУїЁїMDEЁеЁїCAEЃЌМДПЩЕУжЄЃЛ
ЃЈ3ЃЉбгГЄЯпЖЮCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂECЃЌРћгУSASжЄЁїBFCЁеЁїDFMЃЌНјЖјПЩвджЄУїЁїMDEЁеЁїCAEЃЌМДПЩЕУжЄЃЛЃЎ
НтЃКЃЈ1ЃЉЁп![]() гы
гы![]() ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ОљЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЁрBE=EC
Ёп![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃКEF=FCЃЌEFЁЭFC
ЃЈ2ЃЉДцдкEF=FCЃЌEFЁЭFCЃЌжЄУїШчЯТЃК
бгГЄCFЕНMЃЌЪЙFM=CFЃЌСЌНгDMЁЂMEЁЂEC
Ёп![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрDF=FBЃЌ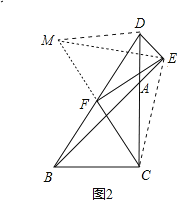
ЁпFC=FMЃЌЁЯBFC=ЁЯDFMЃЌDF=FBЃЌ
ЁрЁїBFCЁеЁїDFMЃЌ
ЁрDM=BCЃЌЁЯMDB=ЁЯFBCЃЌ
ЁрMD=ACЃЌMDЁЮBCЃЌ
ЁрЁЯMDC=ЁЯACB=90Ёу
ЁрЁЯMDE=ЁЯEAC=135ЁуЃЌ
ЁпED=EAЃЌ
ЁрЁїMDEЁеЁїCAEЃЈSASЃЉЃЌ
ЁрME=ECЃЌЁЯMED=ЁЯCEAЃЌ
ЁрЁЯMED+ЁЯFEA=ЁЯFEA+ЁЯCEA=90ЁуЃЌ
ЁрЁЯMEC=90ЁуЃЌгжFЮЊCMЕФжаЕуЃЌ
ЁрEF=FCЃЌEFЁЭFCЃЛ
ЃЈ3ЃЉEF=FCЃЌEFЁЭFCЃЎ
жЄУїШчЯТЃК
ШчЭМ4ЃЌбгГЄCFЕНMЃЌЪЙCF=FMЃЌСЌНгMEЁЂECЃЌСЌНгDMНЛбгГЄНЛAEгкGЃЌНЛACгкHЃЌ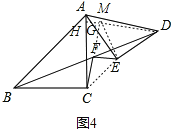
ЁпFЮЊBDжаЕуЃЌ
ЁрDF=FBЃЌ
дкЁїBCFКЭЁїDFMжа
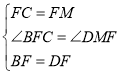
ЁрЁїBFCЁеЁїDFMЃЈSASЃЉЃЌ
ЁрDM=BCЃЌЁЯMDB=ЁЯFBCЃЌ
ЁрMD=ACЃЌspan>HDЁЮBCЃЌ
ЁрЁЯAHG=ЁЯBCA=90ЁуЃЌЧвЁЯAGH=ЁЯDGEЃЌ
ЁрЁЯMDE=ЁЯEACЃЌ
дкЁїMDEКЭЁїCAEжа
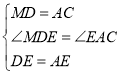
ЁрME=ECЃЌЁЯMED=ЁЯCEAЃЌ
ЁрЁЯMED+ЁЯFEA=ЁЯFEA+ЁЯCEA=90ЁуЃЌ
ЁрЁЯMEC=90ЁуЃЌгжFЮЊCMЕФжаЕуЃЌ
ЁрEF=FCЃЌEFЁЭFCЃЎ

 дФЖСПьГЕЯЕСаД№АИ
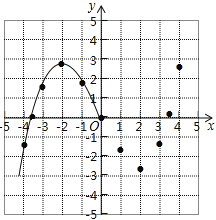
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГбЇЯАаЁзщдкбаОПКЏЪ§y=![]() x3Љ2xЕФЭМЯѓгыаджЪЪБЃЌвбСаБэЁЂУшЕуВЂЛГіСЫЭМЯѓЕФвЛВПЗжЃЎ
x3Љ2xЕФЭМЯѓгыаджЪЪБЃЌвбСаБэЁЂУшЕуВЂЛГіСЫЭМЯѓЕФвЛВПЗжЃЎ
x | Ё | Љ4 | Љ3.5 | Љ3 | Љ2 | Љ1 | 0 | 1 | 2 | 3 | 3.5 | 4 | Ё |
y | Ё | Љ | Љ |
|
|
| 0 | Љ | Љ | Љ |
|
| Ё |
ЃЈ1ЃЉЧыВЙШЋКЏЪ§ЭМЯѓЃЛ
ЃЈ2ЃЉЗНГЬ![]() x3Љ2x=Љ2ЪЕЪ§ИљЕФИіЪ§ЮЊЁЁ ЁЁЃЛ
x3Љ2x=Љ2ЪЕЪ§ИљЕФИіЪ§ЮЊЁЁ ЁЁЃЛ
ЃЈ3ЃЉЙлВьЭМЯѓЃЌаДГіИУКЏЪ§ЕФСНЬѕаджЪЃЎ