题目内容
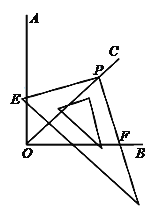
【题目】如图,![]() 平分
平分![]() ,
,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() .
.
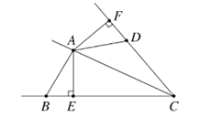
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,
,![]() .求四边形
.求四边形![]() 的面积.
的面积.
【答案】(1)∠CDA=120°;(2)9
【解析】
(1)根据角平分线的性质得到AE=AF,进而证明Rt△ABE≌Rt△ADF(HL),再根据全等三角形的性质即可得到∠CDA的度数;
(2)先证明Rt△ACE与Rt△ACF(HL),得到CE=CF,再得到CE的长度,将四边形![]() 的面积分成△ACE与△ACD的面积计算即可.
的面积分成△ACE与△ACD的面积计算即可.
解:(1)∵![]() 平分
平分![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]()
∴AE=AF,∠AEB=∠AFD=90°,
在Rt△ABE与Rt△ADF中
![]() ,
,
∴Rt△ABE≌Rt△ADF(HL)
∴∠ABE=∠ADF=60°,
∴∠CDA=180°-∠ADF=120°,
故∠CDA=120°.
(2)由(1)可得Rt△ABE≌Rt△ADF
∴BE=DF,
又∵在Rt△ACE与Rt△ACF中
![]()
∴Rt△ACE与Rt△ACF(HL)
∴CE=CF
CE=CF=CD+DF=CD+BE=5,
又∵![]()
∴AF=AE=2
∴四边形AECD的面积=![]()
故四边形![]() 的面积为9
的面积为9

练习册系列答案
相关题目