题目内容
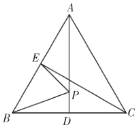
【题目】如图，在
中，
，
、
是的两条中线，
是上一个动点，当点运动到某一位置时，可使△PBE的周长最小，则这个最小值为_____
．
【答案】
【解析】
△PBE的周长=BE+PB+PE，BE为定值，要使周长最小，则PB+PE最小，转化为“将军饮马”问题，当C，P，E三点共线时，PB+PE=CE最小，求出CE即可．
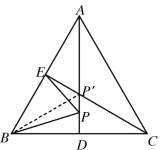
如图设CE与AD交于点P'，连接BP'
∵△PBE的周长=BE+PB+PE，BE为定值，
∴要使周长最小，则PB+PE最小，
∵在
中，
∴△ABC为等边三角形，
又∵AD、CE为中线
∴AD⊥BC，CE⊥AB，
即AD垂直平分BC，
当P点运动到P'时，P'B+P'E=CE最小
在Rt△BCE中，BC=6，BE=
AB=3cm
∴
cm
∴△PBE的周长的最小值= BE+CE=cm
故答案为：．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
