题目内容
【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
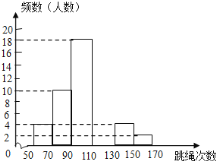
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |
【答案】(1)a=10, b=12;(2)3;(3)![]() ;(4)18
;(4)18
【解析】
(1)根据条形统计图的显示可以得出a,根据总人数减去其他的人数可得到b;
(2)根据中位数的定义可得结果;
(3)用大于130的人数除以总人数可得到结果;
(4)用总数150乘以![]() 可得到结果.
可得到结果.
(1)根据频数分布直方图知:a=10,b=50-4-10-18-4-2=12;
(2)中位数是位置处于中间的数,共50个数据,处于中间的是第25,26个,正好落在第3小组.
(3)根据已知优秀的人数有2+4=6人,所以优秀的概率为:![]() .
.
(4)150![]() =18.
=18.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目