题目内容
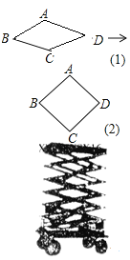
【题目】如图是利用四边形的不稳定性制造的一个移动升降装修平台,其基本图形是菱形,主体部分相当于由6个菱形相互连接而成,通过改变菱形的角度,从而可改变装修平台高度.
(1)如图(1)是一个基本图形,已知AB=1米,当∠ABC为60°时,求AC的长及此时整个装修平台的高度(装修平台的基脚高度忽略不计);
(2)当∠ABC从60°变为90°(如图(2)是一个基本图形变化后的图形)时,求整个装修平台升高了多少米.[结果精确到0.1米]
【答案】(1)AC=1米,整个装修平台的高度为6米 ;(2)整个装修平台升高了![]() 米
米
【解析】
(1)连接图(1)中菱形ABCD的对角线AC、BD,交于O,则利用菱形的对角线互相垂直可得出对角线AC的长度,继而可得出整个平台的高度.
(2)结合(1)的求解方法可求出此时的平台高度,两者相减即可得出答案.
解:(1)连接图(1)中菱形ABCD的对角线AC、BD,交于点O,
在Rt![]() ABO中,∠AOB=90°,∠ABO=
ABO中,∠AOB=90°,∠ABO=![]() ∠ABC=30°,
∠ABC=30°,
∴OA=ABsin∠ABO=1×sin30°=0.5,
此时AC=2AO=2×0.5=1(米),
故可得整个装修平台的高度=1×6=6(米);
(2)当∠ABC从60°变为90°时,AC=![]() ,
,
此时的整个装修平台的高度=![]() ×6≈1.41×6≈8.46,
×6≈1.41×6≈8.46,
整个装修平台升高的高度为8.46﹣6=2.46≈2.5米.


【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
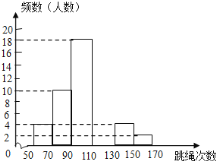
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |