题目内容
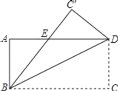
【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

【答案】(4022,6033)
【解析】
根据已知条件可求得点B和点C的坐标,令直线ON的表达式为y=kx,代入A得坐标,可求得k,即得出直线ON的表达式,再根据已知条件求出点B2的值.
设直线OM的解析式为![]() ,
,
已知点A、![]() 、
、![]() 在直线OM上且
在直线OM上且![]() ,
,
把点A代入可得OM的解析式为![]() ,
,
正方形ABXD的边长为1,所以B点的坐标为![]() ,则点C的坐标为
,则点C的坐标为![]() ,
,
∵点C、![]() 、
、![]() 在直线ON上,可解得直线ON的解析式为
在直线ON上,可解得直线ON的解析式为![]() ,
,
设![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线ON上,
在直线ON上,
∴![]() ,
,
∵正方形![]() D的边长为2011,
D的边长为2011,
∴![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线OM上,则
在直线OM上,则![]() ,
,
则![]() ,
,
∴![]() 。
。
解得![]() .
.
则点![]() 的坐标为(4022,6033).
的坐标为(4022,6033).
故答案为(4022,6033).

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
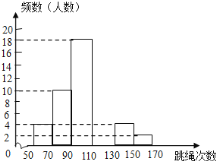
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |