题目内容
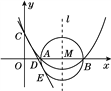
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
,且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边).
(1)求抛物线的表达式及A,B两点的坐标.
(2)在(1)中抛物线的对称轴l上是否存在一点P,使AP+CP的值最小?若存在,求AP+CP的最小值;若不存在,请说明理由;
(3)在以AB为直径的⊙M中,CE与⊙M相切于点E,CE交x轴于点D,求直线CE的表达式.
【答案】 (1) y=![]() x2-
x2-![]() x+2,A(2,0),B(6,0).(2)存在,AP+CP的最小值为2
x+2,A(2,0),B(6,0).(2)存在,AP+CP的最小值为2![]() ;(3)直线CE的表达式为y=-
;(3)直线CE的表达式为y=-![]() x+2.
x+2.
【解析】试题分析:(1)根据知抛物线的顶点坐标,设抛物线的解析式为y=a(x﹣4)2﹣![]() ,再根据抛物线经过(0,2)求出抛物线解析式,进而求出A、B两点的坐标;(2)存在,线段BC的长即为AP+CP的最小值,求得BC的长即可;(3)连接ME,根据已知条件易证△COD≌△MED.根据全等三角形的性质可得OD=DE,DC=DM.设OD=x,则CD=DM=OM-OD=4-x.在Rt△COD中,根据勾股定理列出方程x2+22=(4-x)2.解方程求得x的值,即可得点D的坐标,利用待定系数法求得直线EC的解析式即可
,再根据抛物线经过(0,2)求出抛物线解析式,进而求出A、B两点的坐标;(2)存在,线段BC的长即为AP+CP的最小值,求得BC的长即可;(3)连接ME,根据已知条件易证△COD≌△MED.根据全等三角形的性质可得OD=DE,DC=DM.设OD=x,则CD=DM=OM-OD=4-x.在Rt△COD中,根据勾股定理列出方程x2+22=(4-x)2.解方程求得x的值,即可得点D的坐标,利用待定系数法求得直线EC的解析式即可
试题解析:
(1)由题意可设抛物线的表达式为y=a(x-4)2-![]() (a≠0).
(a≠0).
∵抛物线经过点C(0,2),
∴a(0-4)2-![]() =2,
=2,
解得a=![]() .
.
∴y=![]() (x-4)2-
(x-4)2-![]() ,
,
即y=![]() x2-
x2-![]() x+2.
x+2.
当y=0时,![]() x2-
x2-![]() x+2=0,
x+2=0,
解得x1=2,x2=6,
∴A(2,0),B(6,0).
(2)存在,由(1)知,抛物线的对称轴l为直线x =4.
∵A,B两点关于l对称,
连接CB交l于点P,连接AP,则AP=BP,
∴AP+CP=BC的值最小.
∵B(6,0),C(0,2),
∴OB=6,OC=2.
∴BC=![]() =2
=2![]() .
.
∴AP+CP=BC=2![]() .
.
∴AP+CP的最小值为2![]() .
.
(3)连接ME,∵CE是⊙M的切线,
∴CE⊥ME.
∴∠CEM=90°.
∴∠COD=∠DEM=90°.
由题意,得OC=ME=2,
∠ODC=∠MDE,
∴△COD≌△MED.
∴OD=DE,DC=DM.
设OD=x,
则CD=DM=OM-OD=4-x.
在Rt△COD中,OD2+OC2=CD2,
∴x2+22=(4-x)2.
∴x=![]() .
.
∴D![]() .
.
设直线CE的表达式为y=kx+d(k≠0),
∵直线CE过C(0,2),
D![]() 两点,
两点,
则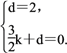
解得
∴直线CE的表达式为y=-![]() x+2.
x+2.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
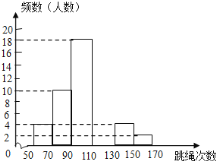
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |