题目内容
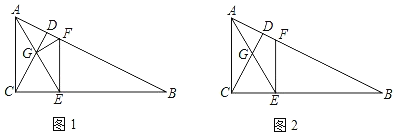
【题目】如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,E为线段BC上一点,AE交CD于G,且GC=GE,EF⊥BC交AB于点F.
(1)求证:AE2=AFAB;
(2)连FG,若BE=2CE,求tan∠AFG;
(3)如图2,当tanB= 时,CE=FE(请直接写出结果,不需要解答过程).
【答案】(1)证明见解析;(2)tan∠AFG=![]() ;(3)
;(3)![]() .
.
【解析】
(1)先证明∠AEF=∠B,然后再证明△AEF∽△ABE,最后根据相似三角形的性质即可证明;
(2)设CE=a.则BE=2a,证明△AEC∽△BAC,得到AC=![]() a,易得∠AFG=60°,最后根据特殊角的三角函数值求解即可;
a,易得∠AFG=60°,最后根据特殊角的三角函数值求解即可;
(3)设BE=a,CE=EF=b,证明 △AEC∽△BAC.得到AC=![]() ,证明△BEF∽△BCA得到a、b的关系,最后根据正切的定义解答即可.
,证明△BEF∽△BCA得到a、b的关系,最后根据正切的定义解答即可.
(1)证明:∵GC=GE,
∴∠GCE=∠GEC,
∵CD⊥AB,
∴∠DCE+∠B=90°,
∵EF⊥BC,
∴∠GEC+∠AEF=90°,
∴∠AEF=∠B,又∠EAF=∠BAE,
∴△AEF∽△ABE,
∴![]() =
=![]() ,
,
∴AE2=AFAB;
(2)设CE=a,则BE=2a,
∵∠DCB+∠B=90°,∠CAB+∠B=90°,
∴∠DCB=∠CAB,
∵∠GCE=∠GEC,
∴∠CAB=∠GEC,又∠ACE=∠BCA=90°,
∴△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC=![]() a,
a,
∴∠CAE=∠BAE=∠AEF=30°,
∴FA=FE,
∵∠GAC=∠GCA=30°,
∴GA=GC,
∵GC=GE,
∴GA=GE,又FA=FE,
∴∠AFG=60°,
∴tan∠AFG=![]() ;
;
(3)设BE=a,CE=EF=b,
∵△AEC∽△BAC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AC2=b(a+b),
∴AC=![]() ,
,
∵EF∥AC,
∴△BEF∽△BCA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
整理得,b2+ab﹣a2=0,
则(![]() )2+
)2+![]() ﹣1=0,
﹣1=0,
解得:![]() =
=![]() ,
,
∴tanB=![]() =
=![]()
故答案为:![]() .
.

【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
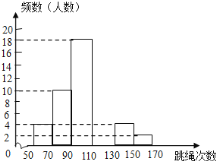
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |