题目内容
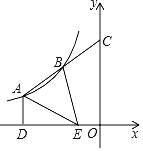
【题目】C,D两城蔬菜紧缺,A,B两城决定支援,A城有蔬菜20吨,B城有蔬菜40吨,C城需要蔬菜16吨,D城需要蔬菜44吨,已知A到C,D的运输费用分别为200元/吨,220元/吨,B到C,D的运输费用分别为300元/吨,340元/吨,规定A向C城运的吨数不小于B向C城运的吨数,设A城向C城运x吨,请回答下列问题:
(1)根据题意条件,填写下列表格:

(2)设总费用为y(元),求出y(元)与x(吨)的函数关系式,并写出x的取值范围;
(3)怎样调运货物能使总费用最少?最少费用是多少?
【答案】(1)①![]() ,②
,②![]() ,③
,③![]() ;(2)
;(2)![]() ,
,![]() ;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
;(3)当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.
【解析】
(1)用C城需要蔬菜的吨数减去x可得①的值;用A城共有的蔬菜吨数减去x可得②的值;用B城共有的蔬菜吨数减去①的值可得③的值;
(2)在(1)的基础上,根据题干已知的运输费用列出等式即可得;再根据“A向C城运的吨数不小于B向C城运的吨数”以及①、②的值均为非负数即可得求出x的取值范围;
(3)根据(2)的结论,利用一次函数的性质即可得.
(1)由题意得:①的值为![]() ;②的值为
;②的值为![]() ;③的值为
;③的值为![]()
故答案为:![]() ,
,![]() ,
,![]() ;
;
(2)由题意得:![]()
整理得:![]()
![]() ①、②的值均为非负数
①、②的值均为非负数
![]()
解得![]()
又![]() A向C城运的吨数不小于B向C城运的吨数
A向C城运的吨数不小于B向C城运的吨数
![]()
解得![]()
综上,x的取值范围是![]() ;
;
(3)由(2)知,![]() ,且
,且![]()
由一次函数的性质可知,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
则当![]() 时,y取得最小值,最小值为
时,y取得最小值,最小值为![]() (元)
(元)
此时,![]() ,
,![]() ,
,![]()
答:当A向C城运8吨,向D城运12吨,B向C城运8吨,向D城运32吨时费用最少,最少费用是17520元.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案【题目】某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).根据图表解答下列问题:
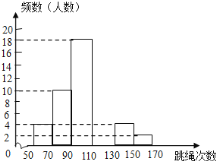
(1)a= ,b= ;
(2)这个样本数据的中位数落在第 组;
(3)若七年级男生个人一分钟跳绳次数x≥130时成绩为优秀,则从这50名男生中任意选一人,跳绳成绩为优秀的概率为多少;
(4)若该校七年级入学时男生共有150人,请估计此时该校七年级男生个人一分钟跳绳成绩为优秀的人数.
组别 | 次数x | 频数(人数) |
第1组 | 50≤x<70 | 4 |
第2组 | 70≤x<90 | a |
第3组 | 90≤x<110 | 18 |
第4组 | 110≤x<130 | b |
第5组 | 130≤x<150 | 4 |
第6组 | 150≤x<170 | 2 |