题目内容
9.解下列方程(Ⅰ)2x2+5x-3=0
(Ⅱ)x2+3=2$\sqrt{3}$x.
分析 (Ⅰ)利用因式分解法解方程;
(Ⅱ)先把方程化为一般式,然后利用因式分解法解方程.
解答 解:(Ⅰ)(2x-1)(x+3)=0,
2x-1=0或x+3=0,
所以x1=$\frac{1}{2}$,x2=-3;
(Ⅱ)x2-2$\sqrt{3}$x+3=0,
(x-$\sqrt{3}$)2=0,
所以x1=x2=$\sqrt{3}$.
点评 本题考查了解一元二次方程-因式分解法:因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
4.某地区某月前两周从周一至周五每天的最低气温是(单位:℃)x1,x2,x3,x4,x5,和x1+1,x2+2,x3+3,x4+4,x5+5,若第一周这五天的平均气温为7℃,则第二周这五天的平均气温为( )
| A. | 7℃ | B. | 8℃ | C. | 9℃ | D. | 10℃ |
18.下列各对数中,相等的一对数是( )
| A. | (-2)3与-23 | B. | -22与(-2)2 | C. | -(-3)与-|-3| | D. | $\frac{{2}^{2}}{3}$与($\frac{2}{3}$)2 |
13.一元二次方程3x2-2x+3=0的根的情况是( )
| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等的正实数根 | D. | 没有实数根 |
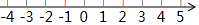 在纸面上有一数轴(如图所示),折叠纸面.
在纸面上有一数轴(如图所示),折叠纸面.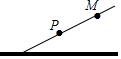 如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是i=1:2.4.
如图是一斜坡的横截面,某人沿着斜坡从P处出发,走了13米到达M处,此时在铅垂方向上上升了5米,那么该斜坡的坡度是i=1:2.4.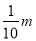 小时,求m的值.
小时,求m的值.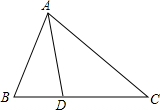 如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.
如图,已知∠BAC=60°,D是△ABC的边BC上的一点,且∠CAD=∠C,∠ADB=80°.求∠B的度数.