题目内容
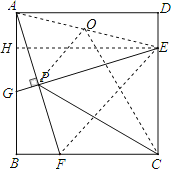
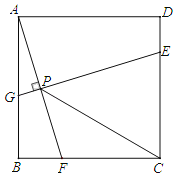
【题目】如图,已知四边形ABCD是边长为4的正方形,E为CD上一点,且DE=1,F为射线BC上一动点,过点E作EG⊥AF于点P,交直线AB于点G.则下列结论中:①AF=EG;②若∠BAF=∠PCF,则PC=PE;③当∠CPF=45°时,BF=1;④PC的最小值为![]() ﹣2.其中正确的有( )
﹣2.其中正确的有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
连接AE,过E作EH⊥AB于H,则EH=BC,根据全等三角形的判定和性质定理即可得到AF=EG,故①正确;根据平行线的性质和等腰三角形的性质即可得到PE=PC;故②正确;连接EF,推出点E,P,F,C四点共圆,根据圆周角定理得到∠FEC=∠FPC=45°,于是得到BF=DE=1,故③正确;取AE 的中点O,连接PO,CO,根据直角三角形的性质得到AO=PO=![]() AE,推出点P在以O为圆心,AE为直径的圆上,当O、C、P共线时,CP的值最小,根据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.
AE,推出点P在以O为圆心,AE为直径的圆上,当O、C、P共线时,CP的值最小,根据三角形的三边关系得到PC≥OC﹣OP,根据勾股定理即可得到结论.
连接AE,过E作EH⊥AB于H,
则EH=BC,
∵AB=BC,
∴EH=AB,
∵EG⊥AF,
∴∠BAF+∠AGP=∠BAF+∠AFB=90°,
∴∠EGH=∠AFB,
∵∠B=∠EHG=90°,
∴△HEG≌△ABF(AAS),
∴AF=EG,故①正确;
∵AB∥CD,
∴∠AGE=∠CEG,
∵∠BAF+∠AGP=90°,∠PCF+∠PCE=90°,
∵∠BAF=∠PCF,
∴∠AGE=∠PCE,
∴∠PEC=∠PCE,
∴PE=PC;故②正确;
连接EF,
∵∠EPF=∠FCE=90°,
∴点E,P,F,C四点共圆,
∴∠FEC=∠FPC=45°,
∴EC=FC,
∴BF=DE=1,
故③正确;
取AE 的中点O,连接PO,CO,
∴AO=PO=![]() AE,
AE,
∵∠APE=90°,
∴点P在以O为圆心,AE为直径的圆上,
∴当O、C、P共线时,CP的值最小,
∵PC≥OC﹣OP,
∴PC的最小值=OC﹣OP=OC﹣![]() AE,
AE,
∵OC=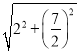 =
=![]() ,AE=
,AE=![]() =
=![]() ,
,
∴PC的最小值为![]() ﹣
﹣![]() ,故④错误,
,故④错误,
故选:C.
![]()