Question

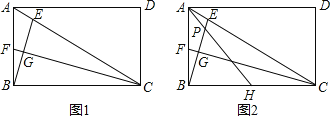
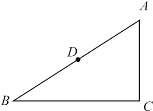
【题目】如图，在Rt△ABC中，∠C=90°，点D是AB的中点，AC＜BC．

(1)试用无刻度的直尺和圆规，在BC上作一点E，使得直线ED平分ABC的周长；(不要求写作法，但要保留作图痕迹)．

(2)在(1)的条件下，若DE分Rt△ABC面积为1﹕2两部分，请探究AC与BC的数量关系．

Answer 1

【答案】(1)作图见解析；(2)BC=3AC

【解析】

（1）在BC上用圆规截取BF=AC，然后再作FC的垂直平分线，其与BC的交点即为E点，最后连接DE即可．

（2）连接DC，由点D是AB的中点，则S△ADC=S△BCD;设S△ADC=S△BCD=x，S△DEC=y，则有（x+y）：（x-y）=2:1，解得x=3y，即E为BC的三等分点，即可说明BC=3EC;有EC=EF=BF=AC,即BC=3AC．

解：（１）如图：DE即为所求；

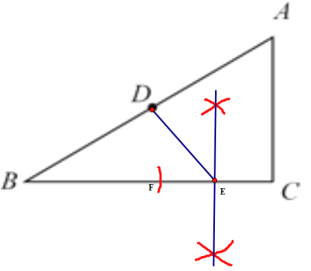
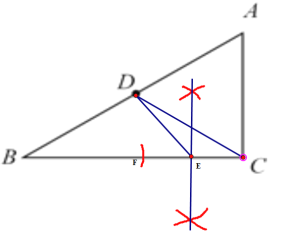
（2）连接DC

∵点D是AB的中点

∴S△ADC=S△BCD

设S△ADC=S△BCD=x，S△DEC=y，

∵S△BDC:S四边形CADE=1:2

∴(S△BDC -S△DCE):( S△ADC+S△DCE)=1:2,

∴2（x-y）=x+y，即x=3y

∴点E为BC的三等分点, 即BC=3EC

∵EC=EF=BF=AC

∴BC=3AC．