题目内容
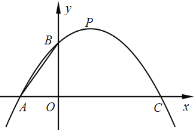
【题目】如图,已知平面直角坐标系,![]() 两点的坐标分别为
两点的坐标分别为![]() .
.
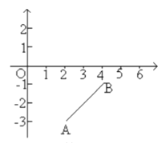
(1)若![]() 是
是![]() 轴上的一个动点,则当
轴上的一个动点,则当![]() _______时,
_______时,![]() 的周长最短;
的周长最短;
(2)若![]() 是
是![]() 轴上的两个动点,则当
轴上的两个动点,则当![]() _______时,四边形
_______时,四边形![]() 的周长最短;
的周长最短;
(3)设![]() 分别为
分别为![]() 轴和
轴和![]() 轴上的动点,请问:是否存在这样的点
轴上的动点,请问:是否存在这样的点![]() , 使四边形
, 使四边形![]() 的周长最短?若存在,请求出,
的周长最短?若存在,请求出,![]() _________,
_________,![]() ________(不必写解答过程);若不存在,请说明理由.
________(不必写解答过程);若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在使四边形
;(3)存在使四边形![]() 周长最短的点
周长最短的点![]() ,
,![]() .
.
【解析】
(1)根据题意,设出并找到点B(4,-1)关于x轴的对称点坐标为(4,1),进而可得直线AB'的解析式,然后得出答案;
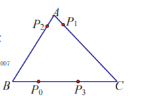
(2)过A点作AE⊥x轴于点E且延长AE,取A'E= AE作点F(1,-1),连接A'F利用两点,间线段最短,可知四边形A BCD的周长最短等于A'F+CD + AB从而确定C点的坐标值;
(3)存在使四边形ABMN的周长最短的点M,N,作A关于y轴的对称点A',作B关于x轴的对称点是AF连接A'B'与x轴,y轴的交点即为点M,N,所以A'(-2,-3), B'(4,1),所以直线A'B'的解析式为:![]() ,从而得到m,n.
,从而得到m,n.
(1)设点B(4,-1)关于x轴的对称点坐标为(4,1),
设直线AB'的解析式为y= kx+ b,
把A(2, -3),B'(4,1)代入得:
![]() ,
,
解得:![]() ,
,
所以y=2x- 7,
令y= 0得![]() ,
,
即![]() ;
;
(2)过A点作AE⊥x轴于点E且延长AE,取A'E= AE,作点F(1,-1),
连接A'F,则A'(2,3),
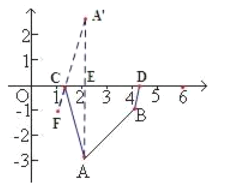
直线A'F的解析式为![]()
即y=4x- 5,
∵C(a,0),且点C在直线A'F上,
∴![]() ;
;
(3)存在使四边形ABMN的周长最短的点M,N;
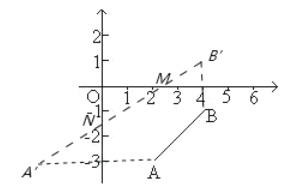
作A关于y轴的对称点A',作B关于x轴的对称点B',连接A'B'与x轴,y轴的交点即为点M,N,设直线A'B'的解析式为:![]() ;
;
∴A'(-2,-3), B'(4,1),
∴直线A'B'的解析式为:![]() ,
,
从而得到![]() ,
,
∴m=![]() ,n
,n![]() .
.