题目内容
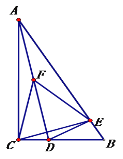
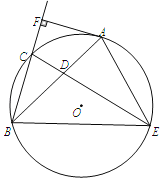
【题目】如图,已知AB是⊙O的弦,点C是弧AB的中点,D是弦AB上一动点,且不与A、B重合,CD的延长线交于⊙O点E,连接AE、BE,过点A作AF⊥BC,垂足为F,∠ABC=30°.
(1)求证:AF是⊙O的切线;
(2)若BC=6,CD=3,则DE的长为 ;
(3)当点D在弦AB上运动时,![]() 的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
的值是否发生变化?如果变化,请写出其变化范围;如果不变,请求出其值.
【答案】(1)见解析;(2)9;(3)不变,![]()
【解析】
(1)如图1中,连接AC,OC,OA.想办法证明OA∥BF即可解决问题;
(2)证明△BCD∽△ECB,推出![]() ,求出CE即可解决问题;
,求出CE即可解决问题;
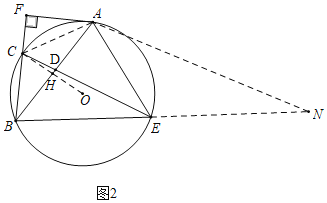
(3)如图2中,连接AC,OC,OC交AB于H,作AN∥EC交BE的延长线于N.证明△ACE∽△ABN,推出![]() 可得结论.
可得结论.
(1)证明:如图1中,连接AC,OC,OA,

∵∠AOC=2∠ABC=60°,OA=OC,
∴△AOC是等边三角形,
∴∠CAO=60°,
∵![]() ,
,
∴AB⊥OC,
∴∠OAD=![]() ∠OAC=30°,
∠OAC=30°,
∵∠ABC=30°,
∴∠ABC=∠OAD,
∴OA∥BF,
∵AF⊥BF,
∴OA⊥AF,
∴AF是⊙O的切线;
(2)解:∵![]() ,
,
∴∠CBD=∠BEC,
∵∠BCD=∠BCE,
∴△BCD∽△ECB,
∴![]() ,
,
∴![]() ,
,
∴EC=12,
∴DE=EC﹣CD=12﹣3=9,
故答案为:9;
(3)解:结论:![]() =
=![]() ,
,![]() 的值不变.
的值不变.
理由:如图2中,连接AC,OC,OC交AB于H,作AN∥EC交BE的延长线于N.
∵![]() ,
,
∴OC⊥AB,CB=CA,
∴BH=AH=![]() AB,
AB,
∵∠ABC=30°,
∴BH=![]() BC,
BC,
∴AC=![]() AB,
AB,
∵CE∥AN,
∴∠N=∠CEB=30°,∠EAN=∠AEC=∠ABC=30°,
∴∠CEA=∠ABC=30°,∠EAN=∠N,
∴∠N=∠AEC,AE=EN,
∵∠ACE=∠ABN,
∴△ACE∽△ABN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() 的值不变.
的值不变.

【题目】为了掌握八年级数学考试卷的命题质量与难度系数,命题组教师赴外地选取一个水平相当的八年级班级进行预测,将考试成绩分布情况进行处理分析,制成如图表(成绩得分均为整数):
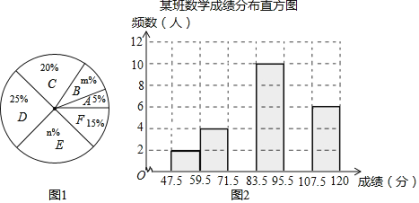
根据图表中提供的信息解答下列问题:
组别 | 成绩分组 | 频数 |
A | 47.5~59.5 | 2 |
B | 59.5~71.5 | 4 |
C | 71.5~83.5 | a |
D | 83.5~95.5 | 10 |
E | 95.5~107.5 | b |
F | 107.5~120 | 6 |
(1)频数分布表中的a= ,b= ;扇形统计图中的m= ,n= ;
(2)已知全区八年级共有200个班(平均每班40人),用这份试卷检测,108分及以上为优秀,预计优秀的人数约为 人,72分及以上为及格,预计及格的人数约为 人;
(3)补充完整频数分布直方图.