题目内容
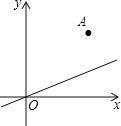
【题目】如图,已知点A(1,1)关于直线y =kx的对称点恰好落在x轴的正半轴上,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
作辅助线,构建点与x轴和y轴的垂线,先根据点A的坐标得出OA′的长,再根据中位线定理和推论得:CF是△AA′E的中位线,所以CF=![]() AE=
AE=![]() ,也可以求OF的长,表示出点C的坐标,代入直线y=kx中求出k的值.
,也可以求OF的长,表示出点C的坐标,代入直线y=kx中求出k的值.
解:设A关于直线y=kx的对称点为A′,连接AA′,交直线y=kx于C,分别过A、C作x轴的垂线,垂足分别为E、F,则AE∥CF,
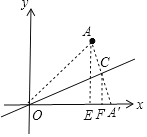
∵A(1,1),
∴AE=OE=1,
∴OA=![]() ,
,
∵A和A′关于直线y=kx对称,
∴OC是AA′的中垂线,
∴OA′=OA=![]() ,
,
∵AE∥CF,AC=A′C,
∴EF=A′F=![]() ,
,
∴CF=![]() AE=
AE=![]() ,
,
∴OF=OA′-A′F=![]() ,
,
∴C(![]() ,
,![]() ),
),
把C(![]() ,
,![]() )代入y=kx中得:
)代入y=kx中得:
![]() ,
,
∴![]() ,
,
故选:B.

练习册系列答案
相关题目