题目内容
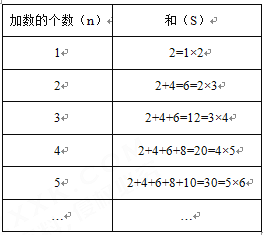
【题目】从2开始,连续的偶数相加,它的和的情况如下表:
(1)当n个最小的连续偶数相加时,它们的和s与n之间的关系式为s= (用含n的式子表示)
(2)并由此计算:
①2+4+6+8+…+50;
②52+54+56+…+100.
【答案】(1)n(n+1);(2)①650;②1900.
【解析】
(1)根据所给的式子可得S与n之间的关系为:S=n(n+1);
(2)首先确定有几个加数,由(1)得出的规律,列出算式,进行计算即可.
(1)∵1个最小的连续偶数相加时,S=1×(1+1),
2个最小的连续偶数相加时,S=2×(2+1),
3个最小的连续偶数相加时,S=3×(3+1),
…
∴n个最小的连续偶数相加时,S=n(n+1);
(2)①根据(1)得:
2+4+6+…+50=25×(25+1)=650;
②52+54+56+…+100,
=(2+4+6+…+50)+50×25,
=25×(25+1)+1250,
=650+1250
=1900.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目