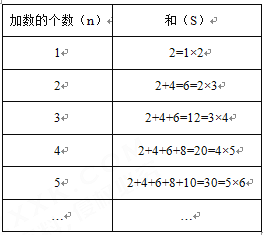
题目内容
【题目】如图,有一段15m长的旧围墙AB,现打算利用该围墙的一部分(或全部)为一边,再用32m长的篱笆围成一块长方形场地CDEF.
(1)怎样围成一个面积为126m2的长方形场地?
(2)长方形场地面积能达到130m2吗?如果能,请给出设计方案,如果不能,请说明理由.
【答案】解:(1)设CD=xm,则DE=(32﹣2x)m,
依题意得:x(32﹣2x)=126,
整理得 x2﹣16x+63=0,
解得 x1=9,x2=7,
当x1=9时,(32﹣2x)=14
当x2=7时 (32﹣2x)=18>15 (不合题意舍去)
∴能围成一个长14m,宽9m的长方形场地.
(2)设CD=ym,则DE=(32﹣2y)m,
依题意得 y(32﹣2y)=130
整理得 y2﹣16y+65=0
△=(﹣16)2﹣4×1×65=﹣4<0
故方程没有实数根,
∴长方形场地面积不能达到130m2 .
【解析】(1)首先设CD=xm,则DE=(32﹣2x)m,进而利用面积为126m2得出等式求出即可;
(2)结合(1)中求法利用根的判别式分析得出即可.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小.
(3)3是方程ax2+(b﹣1)x+c=0的一个根;
(4)当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的个数为( )
A.4个
B.3个
C.2个
D.1个